¿Sabías que se puede utilizar la regularización Lasso en problemas de overfitting?
Lasso es la abreviación de Least Absolute Shringkage and Selection Operator, que en español se traduce como operador de selección y contracción mínima absoluta. La regularización Lasso es, como su nombre indica, un método de reducción y selección de variables para la interpretación del modelo de regresión lineal. Esta es muy aplicada en el aprendizaje automático.
¿Qué es la regularización Lasso?
La regularización Lasso es un método cuyo objetivo es obtener el subconjunto de predictores que minimice el error de predicción para una variable de respuesta cuantitativa. Esta regularización hace esto al imponer una variable de restricción en los parámetros del modelo que hace que los coeficientes de regresión de algunas variables se reduzcan a cero.
La contracción es donde los valores de los datos se reducen hasta un punto central, como la media. Este tipo de regularización es adecuado para modelos que muestran altos niveles de multicolinealidad o cuando desea automatizar ciertas partes de la selección del modelo. El tipo de técnica utilizada es la regularización L1.
Regularización Lasso en problemas de overfitting
La regularización Lasso en problemas de overfitting es casi lo mismo que la regularización Ridge, que es L2. Es decir, L1 y L2 son muy similares, ya que tienen el mismo problema, el mismo enfoque y la solución también es muy parecida. La diferencia es que la función de coste en Lasso, en vez de utilizar los coeficientes al cuadrado, utiliza la norma de los coeficientes multiplicado por alfa. Esto permite crear modelos más simples. Lo demás es exactamente igual.
Veamos la forma matricial de la regularización Lasso en problemas de overfitting:
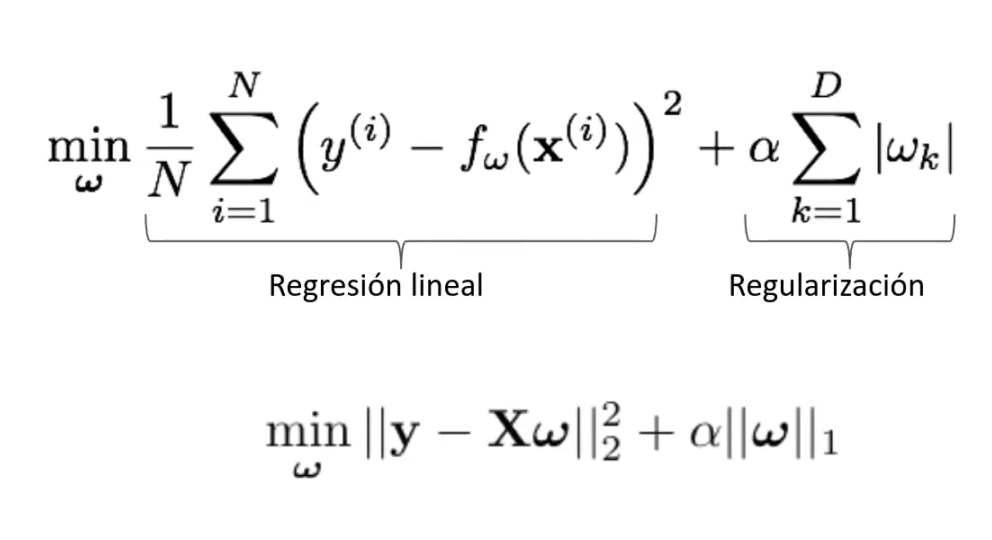
from sklearn import datasets
diabetes = datasets.load_diabetes ()
x = diabetes.data
y = diabetes.target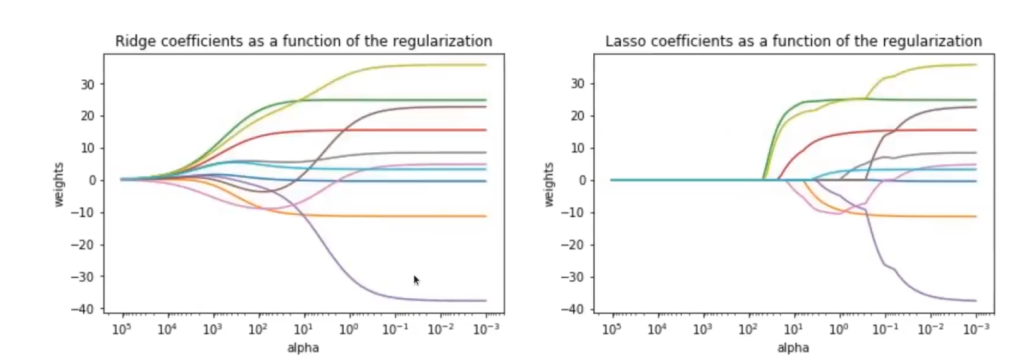
Aquí podemos ver cómo en la regularización Ridge, a media que regularizamos, los coeficientes del modelo van tendiendo a cero.
En la regularización Lasso en problemas de overfitting vemos una cosa que es distinta. ¿Qué está pasando? Que hay un punto en el que se van los coeficientes.
Ridge, entonces, es una bajada suave en la que todos los coeficientes estimados van tendiendo a cero; es una bajada más o menos continua de todo el parámetro de regularización. No obstante, con Lasso sucede que, en algún momento dado, los coeficientes se van anulando. Vemos, por ejemplo, que en 100 con un alfa de 1 hay un parámetro que ya desaparece; no cuenta, es cero. Todos los demás van teniendo unos pesos, pero igual se van desvaneciendo a media que se alarga uno solo de los coeficientes.
Lo que implica este fenómeno es que Lasso está haciendo una selección de características implícitas, porque cuando está en 100, la característica marrón en la imagen, fuera la que fuese, ya no vale nada. Con esto sabemos que, en cierto punto de la regularización, esa característica no es importante y no está aportando valor a nuestro problema.
Esto significa que la regularización Lasso en problemas de overfitting es la mejor o, al menos, una de las mejores opciones si nuestra intención es hacer selección de características. En cambio, si no queremos hacer una selección de características, tenemos que poner cuidado y no utilizar este método, porque automáticamente la regularización Lasso en problemas de overfitting la va a hacer por nosotros.
Regularización Lasso L1 vs. regularización Ridge L2
| Regularización Ridge | Regularización Lasso |
| Forma matricial: | Forma matricial: |
| Afecta a todos los coeficientes (incluye todos o ninguno) | Capaz de anular algunos coeficientes (solución dispersa) |
| Computacionalmente eficiente y previene overfitting | Selección de características e interpretabilidad del modelo |
| Buen punto de partida para analizar un problema: por defecto, usarlo | También previene el overfitting |
Por defecto, la recomendación es que usemos regularización Ridge, porque a pesar de que la regularización Lasso en problemas de overfitting es efectiva para tratarlos, la Ridge es mejor y no nos hace esa selección de características tan forzada. En general, a no ser que nuestra intención específica sea hacer una selección de características, utilizamos Ridge. En caso de no tener mucha claridad al respecto, así nos aseguramos de que solo estamos regularizando.
¿Qué sigue?
Ahora qué has comprendido cómo funciona la efectividad de la regularización Lasso en problemas de overfitting, podemos seguir aprendiendo por medio del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva que te permitirá adquirir todos los conocimientos necesarios para incursionar en uno de los mercados laborales mejores pagados en la actualidad. ¡Sigue aprendiendo, anímate a cambiar tu futuro y solicita más información ahora!











