En un ejercicio anterior habíamos aplicado la regularización por medio de una regresión lineal con tres variables: x0, x1 y x2. Ahora vamos a aplicar una regularización L1 o regularización Lasso en R para ajustar modelos más simples en el ejercicio de regresión lineal.
Ejercicio de regularización Lasso en R
Añadamos el término:
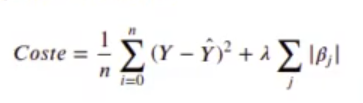
De los coeficientes βj, no tenemos en cuenta la intersección. Ten en cuenta que:
- Cuando λ → 0, entonces βLASSO → βoriginal mínimos cuadrados
- Cuando λ → ∞, entonces βLASSO → 0
Tratamos de minimizar la suma de todos los demás coeficientes del modelo:
In [ ] : lambda <- 40
lambda <- 2
loss_lasso <- function (beta) {
sum ((df$y - myfunction (df [ , - ncol (df)], beta)) ^ 2) / (2 * nrow (df)) + lambda * sum (abs (beta [ -1]))
}
x_historico <- optim_beta (myfunction, loss_lasso, maxiter = 1e4)
In [ ] : options (repr.plot.height = 4, repr.plot.width = 8)
library (ggplot2)
g1 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = betal), color = 'red') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [1], color = 'black')
g2 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta2), color = 'blue') + theme (axis.text.x = element_text(angle = 45)) + geom_hline (yintercept = beta_real [2], color = 'black')
g3 <- ggplot(x_historico, aes (x = step)) + geom_line (aes (y = beta3), color = 'green') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [3], color = 'black')
g4 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta4), color = 'orange') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [4], color = 'black')
library (egg)
grid.arrange (g1, g2, g3, g4, nrow = 1)
La regularización Lasso en R tiene un parámetro que se llama lambda. Ese lambda nos va a decir cuánto peso e importancia hay que darle a la suma de los coeficientes. En el caso anterior, estamos empeorando el error cuadrático medio con el fin de conseguir en el futuro una ganancia en los datos de training. El resultado del código anterior es:
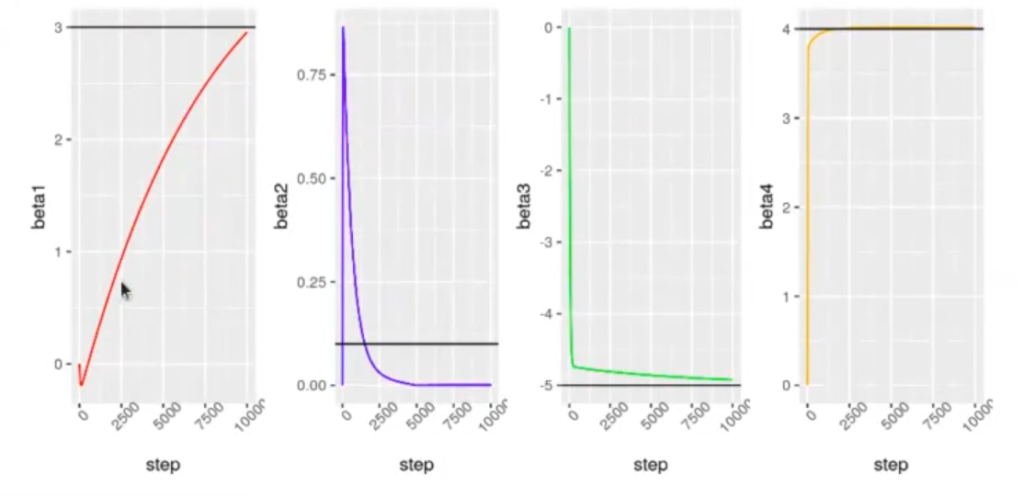
El coeficiente beta2 se lo ha llevado a 0. Beta3 y beta4 siguen más o menos los mismos valores y beta1, al parecer, sigue subiendo y no había alcanzado los números.
Lo interesante de estos modelos es que beta2 ha llegado a 0.
Paquete glmnet para regularización Lasso en R
La regularización Lasso en R descarta los componentes que tienen menos certeza en el resultado final, es decir, los coeficientes con un valor más alto.
En R existe el paquete glmnet, que permite aplicar la regularización a modelos lineales.
Al glmnet le tenemos que pasar una matriz de los datos de entrada y una matriz de lo que queremos predecir; también le pasamos el valor de lambda.
El valor de alpha nos dice que si es 1, es lasso, y si es 0, es ridge.
In [ ] : library (glmnet)
model <- glmnet (as.matrix (df [ , c ('x1', 'x2',' x3' )]), as.matrix (df [ , 'y']), lambda = 2, alpha = 1, standardize = F)
coefficients (model)4 x 1 sparse Matrix of class «dgCMatrix»
s0
(Intercept) : 4.224618
x1 : .
x2 : -4.993921
x3 : 4.021538
¿Qué ha hecho el modelo? Se ha quedado con los coeficientes del intercept y ha mostrado el primer coeficiente (4.224618), el segundo (-4.993921) y el tercero (4.021538).
El coeficiente del x1 ha desaparecido.
¿Para qué sirve este modelo de regularización Lasso en R? Esto sirve para la extracción de características. En este caso, todo parece indicar que la variable x1 no es muy importante.
In [15] : model
Una vez que nos decantamos por una regularización Lasso, ¿cómo obtenemos el valor óptimo de i?
In [ ] : fit <- glmnet (as.matrix(df [ , c ('x1', 'x2', 'x3')]), as.matrix (df[, 'y']), alpha = 1, standardize = F)
par (mfrow = c (1, 3))
grid()
plot (fit, label = TRUE, xvar = "lambda")
grid()
plot (fit, label = TRUE, xvar = "dev")
grid()
#print(fit)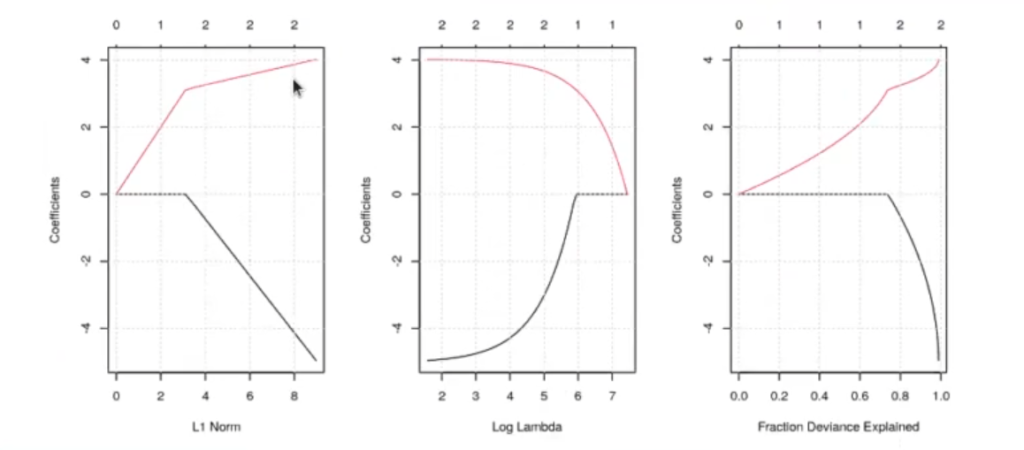
In [18] : #Calculamos los coeficientes para un valor dado de lambda
l <- exp (6.5)
coef (fit, s = l)
#Mostramos el valor de R ^ 2 que se corresponde con la Fracción de la desviación típica explicada
caret::postResample (predict (fit, newx = as.matrix (df[ , c ('x1', 'x2', 'x3')]), s = l), df$y)
RMSE: 54.9089153420216
Rsquared: 0.7752015170
MAE: 45.8563737881608
Podemos ir probando con varios valores de λ hasta encontrar el óptimo en el proceso de regularización Lasso en R.
¿Qué te pareció este post?
Ahora que hemos aprendido cómo funciona la regularización Lasso en R, puedes seguir comprendiendo conceptos del Big Data por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Estarás acompañado de los mejores profesionales, quienes te guiarán en tu proceso de convertirte en un gran experto. ¡Anímate y solicita más información!











