La regularización por restricción en red convolucional (Max norm constraints) es uno de los conocimiento importantes para la regularización de redes profundas convolucionales, puesto que debes contar con el conocimiento de todas las opciones que se encuentran para llevar a cabo esta tarea y saber elegir cuál es la mejor solución para tu procesamiento de los datos.
Por este motivo, en este post, te explicamos qué es y cómo funciona la regularización por restricción en red convolucional en el campo del Deep Learning.
Regularización por restricción en red convolucional
La regularización por restricción en red convolucional o Max norm constraints es uno de los tipos de regularización que se basa, como su nombre expone, en restricciones. Por ejemplo, podríamos establecer un máximo que los pesos no pueden superar.

En la práctica, la regularización por restricción en red convolucional se implementa usando el gradient descent o descenso del gradiente para calcular el nuevo valor de los pesos como lo haríamos normalmente, solo que después se calcula la norma 2 de cada vector de pesos para cada neurona y se pone como condición que no pueda superar a c, es decir: ||W||2<c. Normalmente, c es igual a 3 o 4.
Lo que conseguimos con esta normalización es que la red no «explote», es decir, que los pesos no crezcan desmesuradamente (recuerda que esto es lo que sucede también si usamos un learning rate muy alto).
Veamos esta regularización:
# Prueba con regularización maxnorm
# importamos la capa max_norm
from tensorflow.keras.constraints import max_norm
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
# Definimos una segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
# Definimos una tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_constraint=max_norm(3.)))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) # aquí deberíamos usar un conjunto distinto al de test!!!
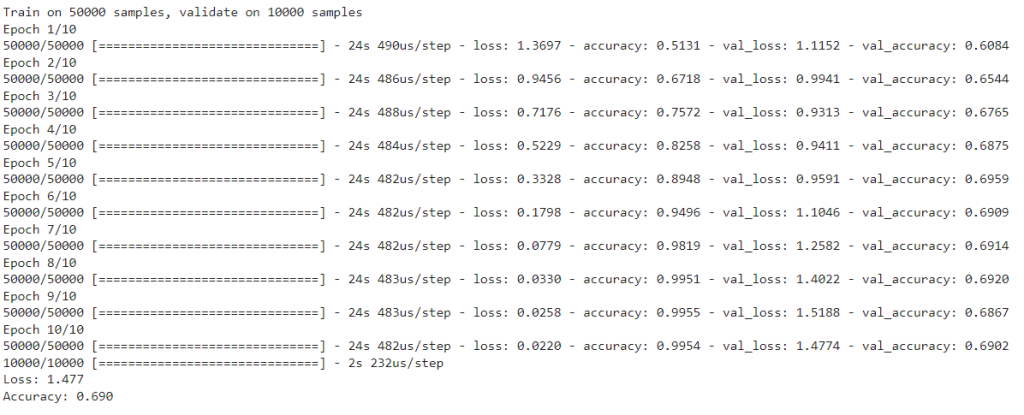
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
En este post, te hemos expuesto qué es y cómo funciona la regularización por restricción en red convolucional dentro del campo del Deep Learning. Sin embargo, ¡todavía queda mucho más por aprender!
Para continuar con tu formación, te recomendamos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, puesto que esta formación intensiva te acercará a muchos más sistemas, lenguajes y herramientas que trabajan con los macrodatos, de forma que te convertirás en un data scientist profesional al saber escoger las mejores alternativas para un procesamiento de datos. ¡Apúntate y triunfa en el sector IT!











