¿Sabes qué es el singular value decomposition y en qué consiste? A continuación te lo mostramos.
Una matriz X con tamaño (m, n) puede expresarse como:
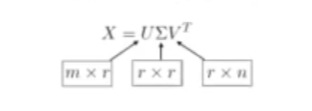
Donde:
- r es el rango de la matriz X.
- U es una matriz (m, r) y ortonormal.
- V es una matriz (n, r) y ortonormal.
- ∑ es una matriz diagonal (r, r), cuyos valores se llaman singular values.
¿Cómo usar singular value decomposition?
Podemos utilizar singular value decomposition de una forma cualitativa. Es decir, nos sirve para extraer información de nuestros datos 2 – O de una forma cuantitativa, así como nos permite reducir la dimensionalidad de nuestra matriz X y seguir manteniendo la información importante.
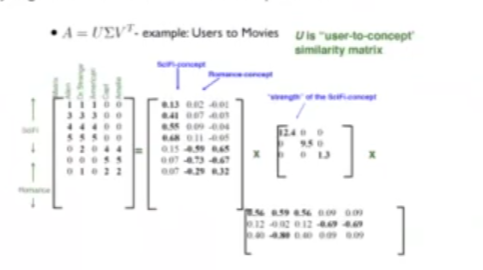
Donde:
- U es una matriz que relaciona: user – concept.
- V es una matriz que relaciona: movie – concept.
- ∑ es la importancia de cada concepto.
Desarrollo del singular value decomposition en Python
#Singular value decomposition
import numpy as np
#user vs movie, a 7 x 5 matrix
A = np.array ([[1, 1, 1, 0, 0],\
[3, 3, 3, 0, 0],
[4, 4, 4, 0, 0],
[5, 5, 5, 0, 0],
[0, 0, 0, 5, 5],
[0, 1, 0, 2, 2]])#Singular value decomposition
U, s, Vt = np.linalg.svd (A, full_matrices = False)
print ("U: \ n", np.round (U, 2))
print ( \nS: \ n", np.round (s, 2))
print ( \nV: \ n", np.round (Vt, 2))U:
[[-0.14 -0.02 -0.01 0.56 -0.38]
[-0.41 -0.07 -0.03 0.21 0.76]
[-0.55 -0.09 -0.04 -0.72 -0.18]
[-0.69 -0.12 -0.05 0.34 -0.23]
[-0.15 0.59 0.65 0. 0.2]
[-0.07 0.73 -0.68 0. 0. ]
[-0.08 0.3 0.33 0. -0.4]]
S:
[12.48 9.51 1.35 0. 0. ]
V:
[[-0.56 -0.59 -0.56 -0.09 -0.09]
[-0.13 0.03 -0.13 0.7, 0.7 ]
[-0.41 0.8 -0.41 -0.09 -0.09]
[-0.71 0. 0.71 0. 0. ]
[ 0. -0. 0. -0.71 0.71]]
#Singular value decomposition
# np.dot (U, np.dot (S, Vt))
A_reconstruida = U.dot (S.dot (Vt))
print (np.round (A_reconstruida, 2))[[ 1. 1. 1. -0. -0. ]
[ 3. 3. 3. -0. -0. ]
[ 4. 4. 4. -0. -0. ]
[ 5. 5. 5. -0. -0. ]
[ -0. 2. -0. 4. 4. ]
[ -0. 0. -0. 5. 5. ]
[ -0. 1. -0. 2. 2. ]]
print (A)[[1 1 1 0 0]
[3 3 3 0 0]
[4 4 4 0 0]
[5 5 5 0 0]
[0 2 0 4 4]
[0 0 0 5 5]
[0 1 0 2 2]]
Otra utilidad que nos proporciona este tipo de descomposiciones es que podemos aplicar una reducción de dimensionalidad a la matriz original y mantener la información relevante.
Ahora vamos a hacerlo con Python:
#Singular value decomposition
print (S.shape)(5, 5)
S.shape [0]5
#Singular value decomposition
list (range (1, S.shape [0]))[1, 2, 3, 4]
A.shape(7, 5)
#Singular value decomposition
U, s, Vt = np.linalg.svd (A, full_matrices = False)
S = np.diag (s)
for n_componentes in range (1, S.shape [0]):
A_hat_reconstructed = U [ : , 0 : n_components]\
.dot (S [ : n_components, :n_components])\
.dot (Vt [ : n_components, : ])\
SSE = np.sum (A - A_hat_reconstructed) ** 2
approx_ratio = n_components / A.shape [1]
comp_ratio = (A.shape [1] * n_components + n_components + A.shape [0] * n_components)
print ("N_components: ", n_components)
print ("\n A reconstruida: \n", np.round (A_hat_reconstructed, 2))
print ("\n SSE: ", SSE)
print ("\n Comp Ratio: ", comp_ratio)
print ("\n---------------------------------------------------\n")N_components: 1
A reconstruida:
[[0.97 1.02 0.97 0.15 0.15]
[2.9 3.05 209 0.46 0.46]
[3.86 4.07 3.86 0.62 0.62]
[4.83 5.09 4.83 0.77 0.77]
[1.07 1.13 1.07 0.17 0.17]
[0.51 0.53 0.51 0.08 0.08]
[0.54 0.57 0.54 0.09 0.09]]
Si cogemos un solo componente, la matriz reconstruida tiene el mismo tamaño que la original, aunque no tiene los mismos valores. Veamos qué pasa con otro número de componentes:


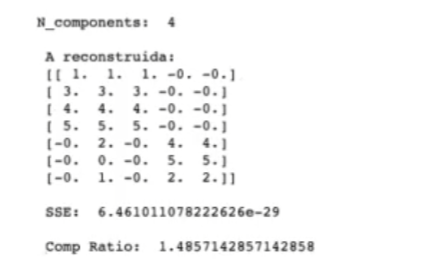
Si quieres seguir aprendiendo, podrás acceder a una de las disciplinas más demandadas y con mejores sueldos de todo el mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Se trata de una formación en la que adquirirás todos los conocimientos para obtener el trabajo de tus sueños. ¡Entra ya para solicitar información e impulsa tu carrera!











