¿Qué son los tests estadísticos para el manejo Big Data?

El análisis exploratorio de datos es el primer paso que todo data scientist tiene que tomar. Para ello es fundamental tener un buen conocimiento de estadística que le permite saber si ciertas variables tienen relación o no, o si varios grupos de datos se pueden considerar diferentes o
iguales. Un buen análisis estadístico nos proporcionará respuestas que pueden complementar algún modelo posterior de machine learning más complejo.

Los tests estadísticos para el manejo Big Data forman parte de la estadística que facilita el desarrollo de un estudio que arroje resultados acertados sobre el valor de los datos para establecer rutas de acción y hacer una toma de decisiones a partir de ello.

Por medio de este post, te explicamos qué son los tests estadísticos para el manejo Big Data y cómo funciona cada uno de ellos.

¿Qué son los tests estadísticos para el manejo Big Data?

Los tests estadísticos para el manejo Big Data funcionan como procesos que testean determinada muestra de datos para llevar a cabo una hipótesis sobre la información procesada.

Ahora, los tests estadísticos poseen divisiones y subdivisiones según la hipótesis que quiera presentarse:

• Por dos grupos: este se divide para comparar la media y la varianza que, a su vez, poseen ciertos tests como T-student y el Barlett.
• Varios grupos: como el test ANOVA o el Turkey.
• Tablas de contingencia: como el Chi cuadrado y el test exacto de Fisher.
• Test de bondad: cuenta con el Test Kolmogorov-Smirnov y el Chi cuadrado.

Algunos tests estadísticos

T-test de student

El origen de este test se remonta a 1908, a la fábrica de cerveza Guiness, y se usa cuando tienes dos grupos de datos y quieres saber si la media de ambos grupos es igual o no. Se tienen dos hipótesis:

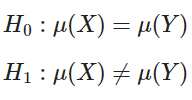
Empieza con las siguientes suposiciones:

• Las muestras han sido seleccionas por muestreo aleatorio simple dentro de la población.
• Las poblaciones siguen una distribución normal.
• Ambas poblaciones tienen la misma varianza.
• Las poblaciones no están correlacionadas.

Primero se calcula la media y varianza de ambos grupos. El test para verificar si la hipótesis nula es cierta puede calcularse como sigue:

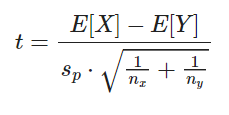
Donde Sp es la desviación estándar compuesta, calculada como:

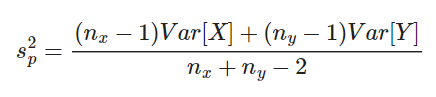
Donde nx y ny son los números de muestras en cada uno de los grupos muestreados. El número de grados de libertad es d. f. = nx + ny – 2. Se asume que las dos varianzas son iguales si ambas pasan el test de varianza de Fisher (F-test).

‘El estimador t-estadístico es: 1.17133980760839’

‘La probabilidad de que por puro azar el estimador t sea mayor de 1.17133980760839 : 0.1319’
‘La probabilidad de que por puro azar el estimador t sea menor de -1.17133980760839 : 0.1395’
‘La probabilidad de que E[X] != E[Y]: 0.2714’

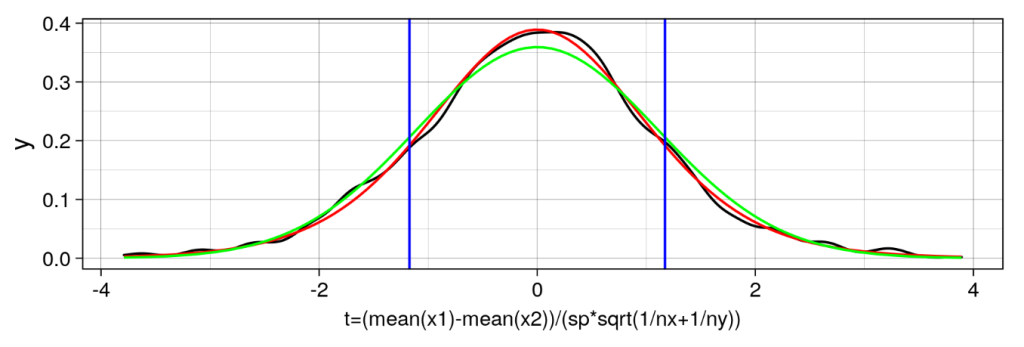
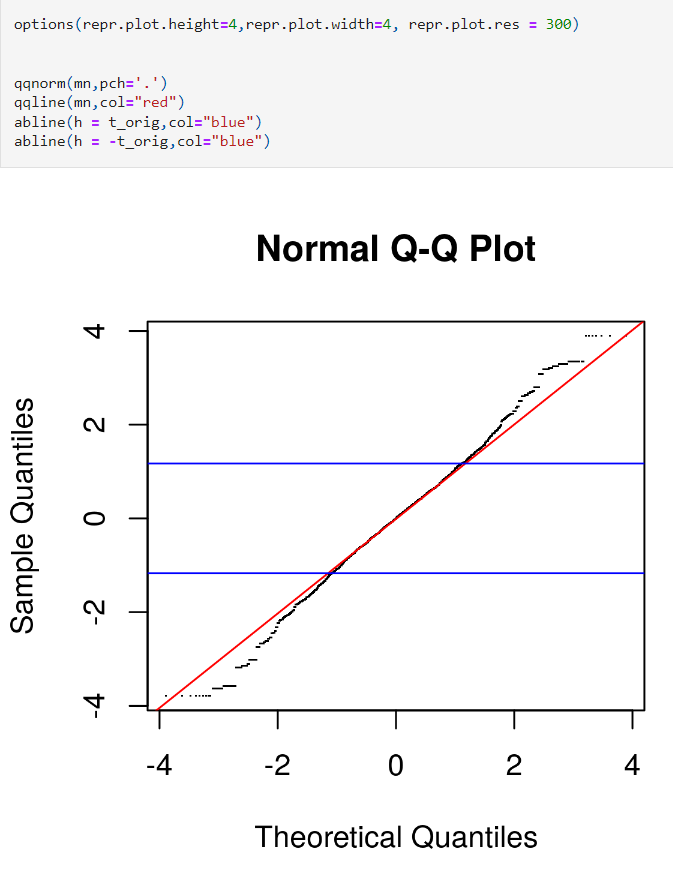
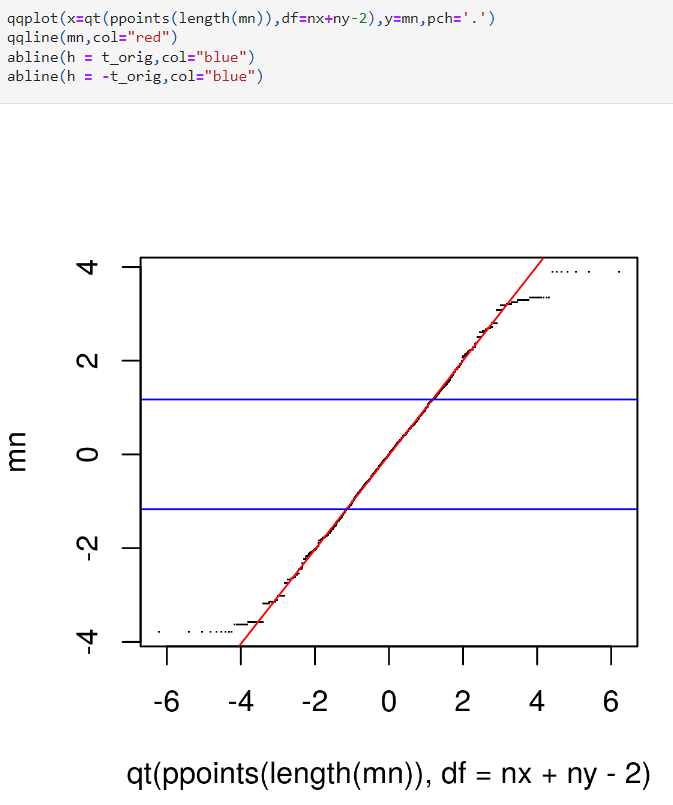
Como vemos, la diferencia de las medias normalizada de estas variables siguen una distribución t-student.

library(ggplot2)
d.f.<-20

loth<-qt(0.025,d.f.,lower.tail = T)
upth<-qt(0.025,d.f.,lower.tail = F)

paste("El margen que nos interesa está en el rango: [",
      round(loth,2),",",round(upth,2),"]")


qsd009<-function(x){    
    out<-dt(x,d.f.)
    out[x> loth  & x<upth  ]<-NA
    out
}
options(repr.plot.height=3,repr.plot.width=6)
xdf<-data.frame(z=c(-4,4))
ggplot(xdf,aes(x=z))+stat_function(fun=dt,args = list(df = d.f.))+
  stat_function(fun=qsd009, geom="area",fill="red")+
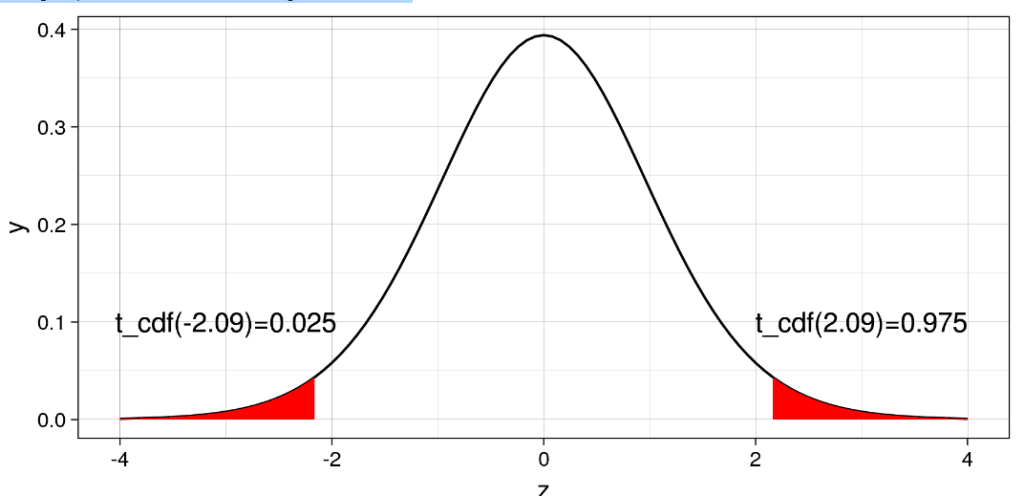
  geom_text(x=3,y=0.1,size=4,label=paste0("t_cdf(",round(upth,2),")=0.975"))+
  geom_text(x=-3,y=0.1,size=4,label=paste0("t_cdf(",round(loth,2),")=0.025"))+
  theme_linedraw()
options(repr.plot.height=7,repr.plot.width=7)

‘El margen que te interesa está en el rango: [ -2.09 , 2.09 ]’

Funciones en R
Supongamos que tienes dos variables aleatorias X e Y, y ahora quieres saber si ambas proceden de la misma población. Una forma de saberlo es calcular la media de X e Y. A continuación, calcula el test t-student y ver el p-valor.

• Un valor muy bajo, por ejemplo inferior a 0.05, te llevaría a rechazar la hipótesis nula y afirmar que las medias son tan diferentes que probablemente vendrán de poblaciones distintas.
• Un p-valor alto te indicaría que la hipótesis es posible que sea cierta.

Test bilateral

‘Media X: 7.22387693229149’
‘Media Y: 4.68409720848552’
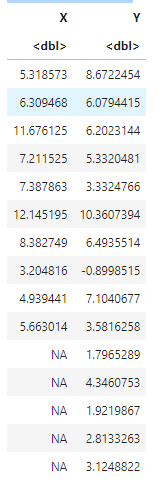
A data.frame: 15 × 2

sp<-sqrt(((nx-1)*var(X)+(ny-1)*var(Y))/(nx+ny-2))
t<-(mean(X)-mean(Y))/(sp*sqrt(1/nx+1/ny))
paste("El estadístico t vale:",t)

‘El estadístico t vale: 2.15402713380947’
Ya que el estadístico t sigue una distribución t-student, tendrás que averiguar cuál es la probabilidad de que haya acabado con ese valor.

pvalue<-(1-pt(abs(t),nx+ny-2))*2

print(paste("El pvalor es",pvalue))

[1] “El pvalor es 0.0419527692505857″
Si el p-valor es bajo (menor de 0.05) significa que es bastante improbable que las medias de X e Y sean iguales. Por lo tanto, en ese caso, podríamos rechazar la hipótesis nula.

El mismo procedimiento se ejecuta usando la función t.test:

t.test(X,Y,var.equal = TRUE)

Two Sample t-test

‘El margen que nos llevaría a rechazar la hipótesis nula está fuera del rango: [ -2.1 , 2.1 ]’

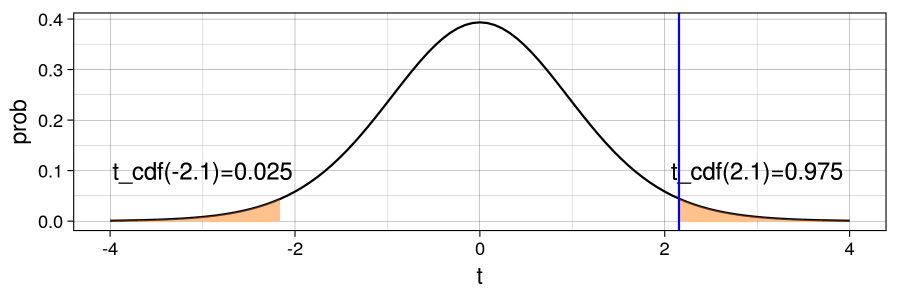
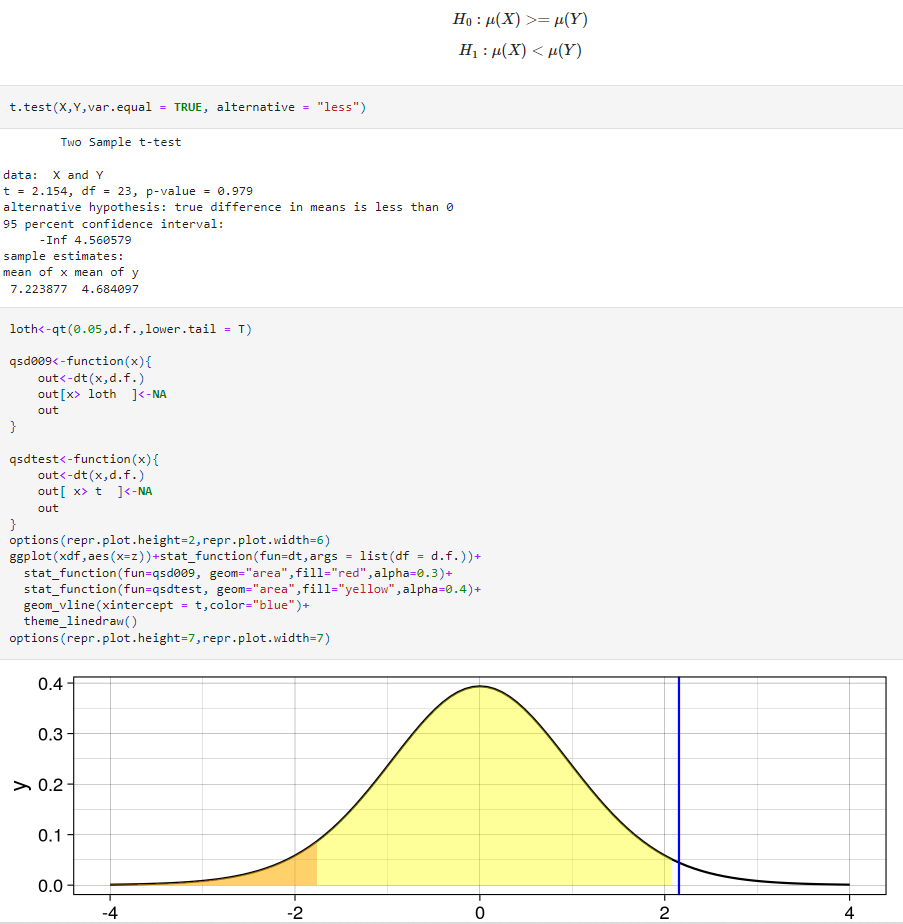
Test unilateral (izquierda)

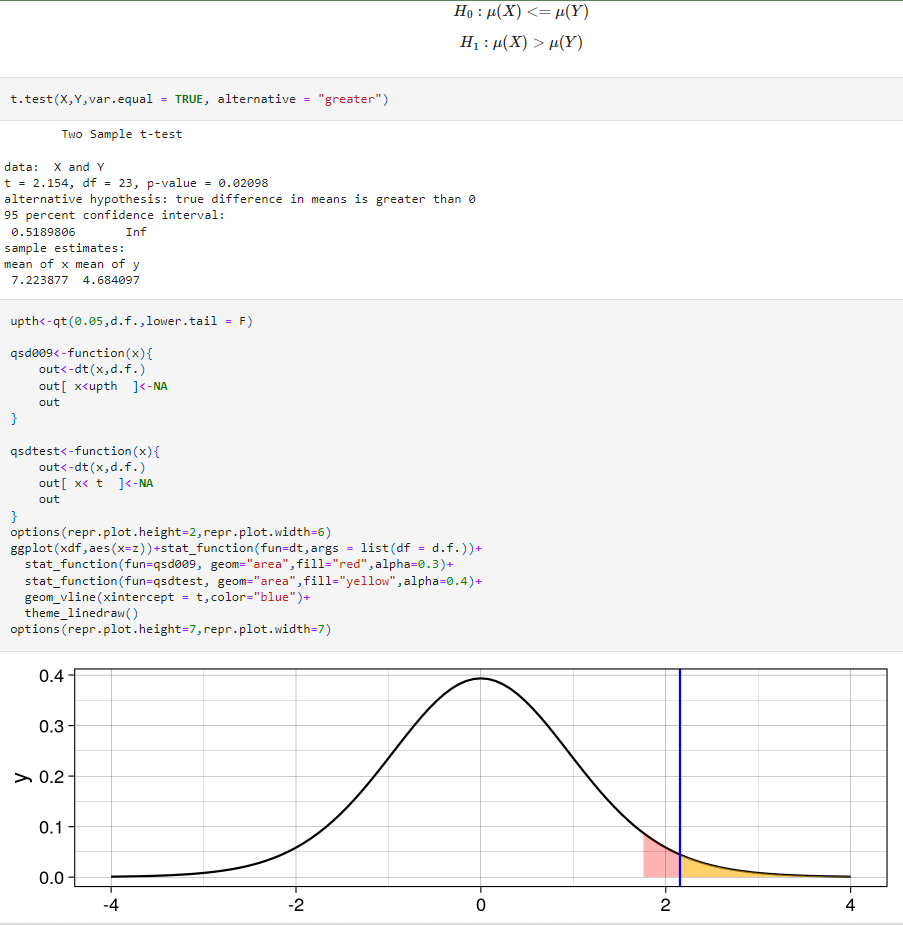
Test unilateral (derecha)

Instrúyete más sobre el Big Data

En el desarrollo de este post, te explicamos qué son los tests estadísticos para el manejo Big Data y cómo funciona cada uno de ellos para el desarrollo de un estudio estadístico en el procesamiento de los macrodatos. Ahora, si planeas instruirte más sobre el Big Data, el Bootcamp Full Stack Big Data, Inteligencia Artifcial & Machine Learning es perfecto para ti, ya que te ayudará a convertirte en un profesional del sector IT.

Con la guía de este bootcamp, podrás llegar a aprender los fundamentos en herramientas y sistemas que se expondrán por módulos y con el acompañamiento constante de profesionales en el manejo de los macrodatos desde las diferentes alternativas. En suma, este proceso te llevará menos de nueve meses. ¡No lo dudes más, solicita información y apúntate ahora!