La unidad tipificada (Z-score) en estadística Big Data forma parte de la gran variedad de funciones que puedes usar para llevar a cabo un estudio estadístico de los macrodatos. A pesar de que cuentas con una serie de saberes sumamente amplios, esta es una de las funciones necesarias cuando se trata de una distribución gaussiana.
En efecto, este tipo de distribución, también conocida como distribución normal, es la más empleada en estadística y su importancia radica en el uso del teorema central del límite. Por esta razón, en este post, te explicamos a qué hace referencia la unidad tipificada (Z-score) en estadística Big Data.
Unidad tipificada (Z-score) en estadística Big Data
La unidad tipificada (Z-score) en estadística Big Data hace referencia al número de desviaciones típicas sobre la media en la que se encuentra el valor que hayas seleccionado con anterioridad.
Por otra parte, la unidad tipificada (Z-score) en estadística Big Data se representa a partir de la siguiente fórmula:
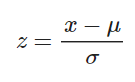
De manera que z es el resultado que se espera calcular a partir de x valor de la población de los datos analizado menos la media μ sobre la desviación típica presentada. Según este resultado, podrás identificar qué tipo de unidad tipificada se encuentra en los macrodatos, puesto que la unidad tipificada (Z-score) en estadística Big Data puede ser positiva o negativa según se encuentre sobre o por debajo de la media.
Por último, hay que tener en cuenta que para ello debes saber primero cuál es la media de los datos que se están estudiando. Además, de la mano de este cálculo, podrás encontrar la función Q(z) que te presentamos a continuación:
Función Q(z)
La función Q(z) es la probabilidad de que una variable aleatoria gaussiana obtenga un valor mayor que x desviaciones típicas por encima de la media. De manera que esta se conoce como un tipo de unidad tipificada (Z-scores) positiva y su fórmula es la siguiente:
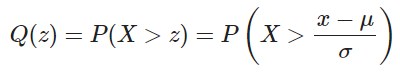
Ahora, si supones que la media es 0, entonces:
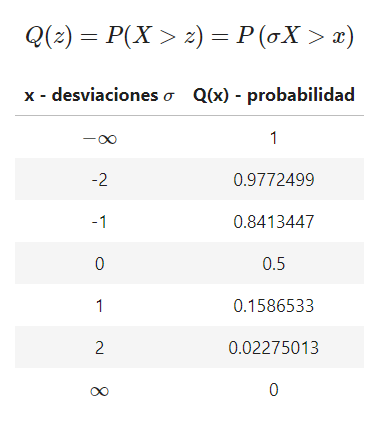
print("En R se calcula con pnorm:")
pnorm(1,lower.tail = F)
print("La inversa se calcula con qnorm:")
qnorm(0.158655,lower.tail = F)
[1] «En R se calcula por medio de la operación pnorm:»
0.158655253931457
[1] «Mientras la inversa se calcula a partir de qnorm:»
1.00000104943105
require(ggplot2)
options(repr.plot.height=4,repr.plot.width=6)
plot_qz<-function(l1,l2){
qnorm1sd<-function(x){
out<-dnorm(x)
out[x< l1]<-NA
out
}
qnorm05sd<-function(x){
out<-dnorm(x)
out[x<l2]<-NA
out
}
qval1<-round(pnorm(l1,lower.tail = F),3)
qval2<-round(pnorm(l2,lower.tail = F),3)
xdf<-data.frame(z=c(-4,4))
ggplot(xdf,aes(x=z))+stat_function(fun=dnorm,args = list(mean = 0, sd=1))+
stat_function(fun=qnorm1sd, geom="area",fill="red")+
geom_text(x=l1+1,y=dnorm(l1),size=4,label=paste0("Q(",l1,")=",qval1))+
stat_function(fun=qnorm05sd, geom="area",fill="green",alpha=0.2)+
geom_text(x=l2+1,y=dnorm(l2),size=4,label=paste0("Q(",l2,")=",qval2))
}
l1<-1 l2<- -0.4 plot_qz(l1,l2)
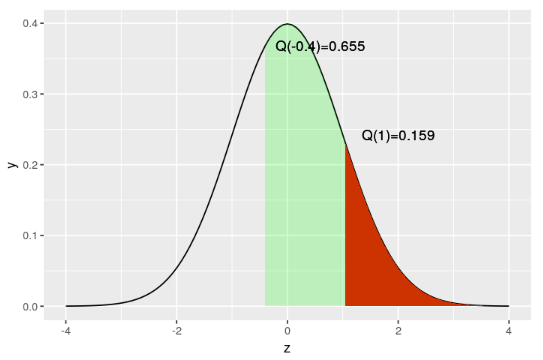
En el desarrollo de este post, te has familiarizado con la unidad tipificada (Z-score) en estadística Big Data. No obstante, el desarrollo de esta función y su traducción gráfica exigen de un gran periodo de práctica para conseguir que sea satisfactoria y, por esta razón, te recomendamos continuar con tu proceso de aprendizaje por medio de la práctica.
Si quieres continuar formándote en este ámbito hasta convertirte en un experto, desde KeepCoding te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, que te instruirá de forma teórica y práctica en cada una de estas herramientas y sistemas para transformarte en un data scientist profesional.
En efecto, podrás llegar a aprender los fundamentos en herramientas y sistemas como el Machine Learning, la Estadística, el Data Mining, la Modern Exploration & Visualization, entre muchos otros que se expondrán por módulos y con el acompañamiento constante de profesionales en el manejo de los macrodatos. ¡No lo dudes más, solicita información y apúntate ahora!











