Visualización de una combinación lineal

En este artículo vamos a hacer la visualización de una combinación lineal entre vectores:

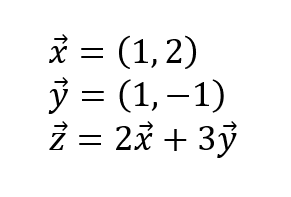
Visualización de una combinación lineal

#Visualización de una combinación lineal
%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
import scipy.sparse as sp
import scipy.sparse.linalg
import scipy.linalg as la
import sympy

#imprimir con notación matemática.
sympy.init_printing (use_latex = 'mathjax')

Funciones para visualizar los vectores

#Visualización de una combinación lineal
def move_spines ():
" " " Crea la figura de pyplot y los ejes. Mueve las líneas de la izquierda y de abajo para que se intercepten con el origen. Elimina las líneas de la derecha y la de arriba. Devuelve los ejes." " "
fix, ax = plt.subplots ()
for spine in ["left", "bottom"] :
      ax.spines [spine].set_position ("zero")

for spine in ["right", "top"] :
      ax.spines [spine].set_color ("none")

return ax

def vect_fig (vector, color):
" " " Genera el gráfico de los vectores en el plano " " "
v = vector
ax.annotate (" ", xy = v, xytext = [0, 0], color = color,
arrowprops = dict (facecolor = color,
shrink = 0,
alpha = 0.7,
width = 0.51)

ax.text(1.1 = v [0], 1.1 * v [1], v)

Para el ejercicio anterior:

#Visualización de una combinación lineal
print (v1)
print (v2)
print (z)

[1 2]

[1 -1]

[5 1]

Ahora, en vez de sumar los componentes directamente, vamos a guardar en las variables z1 y z2 los resultados:

#Visualización de una combinación lineal
z1 = 2 * v1
z2 = 3 * v2

print ("Primer componente de la suma: ", z1)
print ("Segundo componente de la suma: ", z2)

Primer componente de la suma: [2 4]

Segundo componente de la suma: [3 -3]

Representamos los componentes del resultado anterior:

#Visualización de una combinación lineal
ax = move_spines ()
ax.set_ylim (-5, 5)
ax.set_xlim (-5, 5)
ax.grid ()

vecs = [z1, z2]
for v in vecs:
      vect_fig (v, "blue")

v = z1 + z2
vect_fig (v, "red")

ax.plot ([z1[0], v[0], [z1[1], v[1]], linestyle = ' -- ')
ax.plot ([z2[0], v[0], [z2[1], v[1]], linestyle = ' -- ')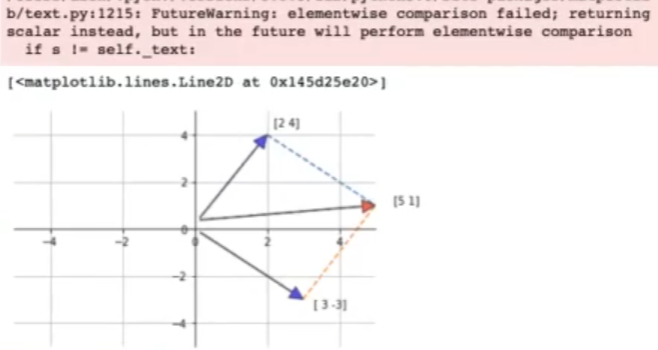

Si los vectores no están centrados es por la función spines de matplotlib; hay que ajustar la escala y los límites de los ejes para poder visualizarlo correctamente. Para el propósito de visualizar la combinación lineal, no es relevante.

Ahora que hemos visto cómo funciona la estructura de un espacio vectorial, puedes seguir aprendiendo sobre Big Data, una de las disciplinas más demandadas y con mejore sueldos de la actualidad. Para conseguirlo tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación de alta intensidad en la que podrás adquirir todos los conocimientos prácticos y teóricos necesarios para triunfar en el mercado laboral en pocos meses. ¡Anímate a impulsar tu carrera y solicita más información ahora!