En este artículo realizaremos un ejercicio de similitud entre vectores. La similitud entre vectores o similitud del coseno es una medida que se utiliza para calcular la similitud entre dos o más vectores. Su expresión es:
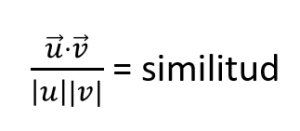
A continuación vamos a plantear dos casos y lo que haremos es calcular la similitud de los vectores de ambos casos, lo cual nos ayudará a entender un poco mejor la ecuación.
Ejercicio de similitud entre vectores
Caso 1
En este primer caso de nuestro ejercicio de similitud entre vectores tenemos que el módulo del vector u es igual a 5 y que el módulo del vector v es igual a 8, es decir, un vector es más largo que otro. Además de eso, el ángulo que separa ambos vectores es igual a 20°.
Matemáticamente, nuestro primer ejercicio de similitud entre vectores se vería representado así:
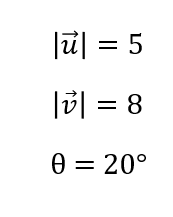
Veamos su representación gráfica:
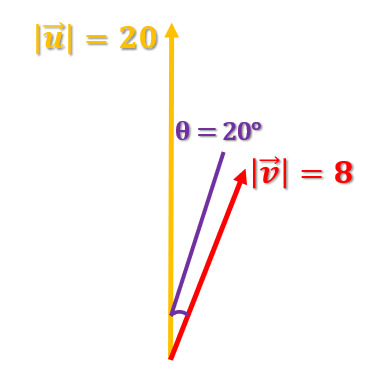
Caso 2
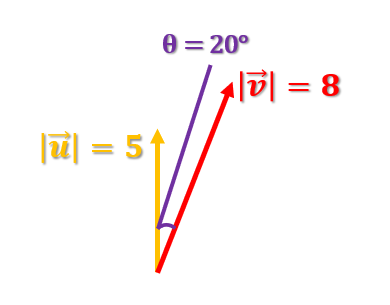
En el segundo caso de nuestro ejercicio de similitud entre vectores tenemos que el módulo de u es igual a 20 y que el módulo de v, en este caso, es igual a 8. Es decir, v sigue igual, el único que ha crecido es el vector u. Asimismo, el ángulo de theta sigue siendo 20, el mismo que en el caso anterior.
Matemáticamente sería:
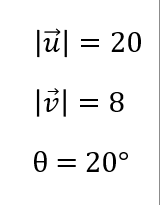
Ahora veamos cómo quedaría la representación gráfica de estos dos vectores con su respectivo ángulo en nuestro ejercicio de similitud entre vectores:
Ahora, cabe preguntar: con base en la ecuación que teníamos al inicio, en donde el vector u multiplicado por el vector v se divide entre el resultado de los módulos de los vectores u y v, ¿es posible que los dos vectores tengan la misma similitud? ¿Puede suceder que la similitud sea igual en ambos casos, aún teniendo en cuenta que el módulo del vector u cambia significativamente en el caso dos, extendiéndose 3 veces más que en el primer caso?
Recordemos que, en esta ecuación, solo tenemos los valores de la parte de abajo, es decir, los valores de los módulos de |u| y |v|. Los valores de los componentes no los tenemos, esto es, el producto escalar lo desconocemos en la ecuación, ya que el producto escalar es la multiplicación de los componentes del vector.
En este ejercicio de similitud entre vectores la similitud es igual en los dos casos, pero es igual porque estamos normalizando la expresión.
Si nos fijamos bien, lo que estamos haciendo es dividir entre el módulo de los vectores. ¿Qué efecto produce esa división entre el módulo de los vectores? En este caso, nos da igual si un vector es muy largo y otro es muy cortito; no nos importa el módulo, la longitud de los vectores es indiferente. Lo único que nos importa es el producto escalar y el ángulo que tienen entre ellos.
Entonces, al hacer la división entre el módulo de cada vector, estamos normalizando. Normalizar no es más que estandarizar. Esto nos permite quitarnos de encima la variable, lo que significa que no nos tenemos que preocupar de si un vector es más largo que otro. Normalizamos, pero la similitud es igual.
A tener en cuenta en la similitud entre vectores
Cabe resaltar la definición del módulo de vector. El módulo del vector, a grandes rasgos, es la longitud que tiene el vector. Si tenemos un vector en un eje de coordenadas que va de A a B, el módulo de ese vector sería la longitud existente entre A y B y la notación para ese módulo estaría marcada por los signos | |, en cuyo caso el módulo de A y B quedaría como |AB|. El módulo del vector también puede utilizarse con múltiples componentes, no solo con uno o dos.
Como podemos observar, este tipo de temáticas son muy empleadas en el campo del machine learning, especialmente en deep learning y redes neuronales. El Big Data es una de las disciplinas más demandadas de la actualidad y mejor pagadas. Por eso tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que podrás adquirir todos los conocimientos necesarios para incursionar en el mercado laboral. ¡Anímate a seguir cambiando tu futuro y entra ahora para informarte!











