Entrenar un modelo Lasso para distintos valores de α

En este artículo veremos cómo entrenar un modelo Lasso para distintos valores de α.

Formulación Lasso

Recordemos que la regularización Lasso se refiere al modelo de regresión lineal con penalización (norma 1) sobre la magnitud de los coeficientes.

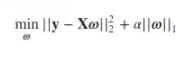
Donde llωll₁ = lω₁l + lω₂l + … + lω_Dl, siendo D el número de atributos (ω₀ no se tiene en cuenta en esta penalización).

Con esta formulación el algoritmo Lasso permite activar o desactivar coeficientes, de forma que se desactivan primero los coeficientes asociados a los atributos que menos influyen en la función de coste (función a minimizar anterior). De este modo:

1. Se previene el overfitting al poder utilizar modelos con menos variables (las desactivamos).
2. Se gana interpretabilidad al poder ver cómo evolucionan las variables supervivientes.

La activación y desactivación de variables está determinada por el parámetro de regularización α, de la misma forma que sucede con el algoritmo Ridge:

• Si α = 0, el resultado se asemeja a un modelo de regresión lineal. Pero cuidado, no será igual, ya que skleam trata de forma diferente Lasso con α = 0 y la regresión lineal. Puedes hacer pruebas y verás cómo Lasso aplica una regularización, incluso con alfas muy pequeños
• Si α → ∞, el valor de todos los coeficientes será nulo.

Entrenar un modelo Lasso: ejercicio

Para entender mejor cómo funciona esto de entrenar un modelo Lasso, veamos un ejemplo:

#Entrenar un modelo Lasso
from sklearn. linear model import Lasso

alpha = 1e - 20
lasso = Lasso (alpha = alpha).fit (X_train, y_train)
w = lasso.coef
norm_w2 = np.dot (w, w.T)

#prediccion
y_hat = lasso.predict (X_test)

#error
error_test = np.mean (np.power (y - y_hat, 2))

plt.plot (x, g_x, 'r', label = '$y$')
plt.plot (x_i, y_i, 'b.', label = '$y_i$')
plt.plot (x, y_hat, 'g', label = '$\hat {y} $')
plt.title ('Grado: %i, MSE: %.2f\nalpha: %g, $ l l w l l_2 ^ 2$ ∞ %.2g' % (degree, error_test, alpha, norm_w2))
plt.legend ()
plt.xlim (0, 1))
plt.ylim ((-2, 2))
plt.show ()

coef_names = ['w' + str (i) + ' :  ' for i in range (1, degree + 1)]

for f, wi in zip (coef names, w):
print (f, wi)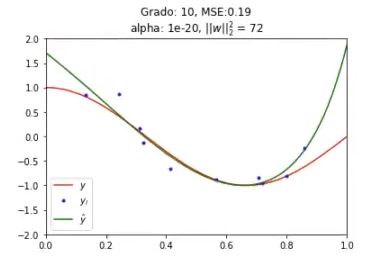

w1: 0.0

w2: -4.7290695741439635

w3: -3.225278493297372

w4: 4.006113165814608

w5: 3.503938970691009

w6: 1.06506245474576

w7: -0.8029528036241889

w8: -1.446054850032147

w9: -0.9547476318503947

w10: 0.39623090019268065

#Entrenar un modelo Lasso
n_alphas = 20
alphas = np.logspace (-10, -3, n_alphas)

coefs = [ ]

norm2_coefs = [ ]
for a in alphas:
lasso = lasso (alpha = a).fit (x_train, y_train)

coefs.append (lasso.coef)
norm2_coefs.append (np.dot (lasso.coef_, lasso.coef_.T))

# Display results
plt.figure (figsize = (14, 5))

ax = plt.subplot (1, 2, 1)
ax.plot (alphas, coefs)
ax.set_xscale ('log')
ax.set_xlim (ax.get_xlim () [ : : - 1]) #reverse axis
plt.xlabel ('alpha')
plt.ylabel('$w_i$')
plt.title ('Coeficientes en función de la regularización')
plt.axis ('tight')

ax = plt.subplot (1, 2, 2)
ax.plot (alphas, norm2_coefs)
ax.set_xscale ('log')
ax.set_xlim (ax.get xlim () [ : : - 1]) #reverse axis 
plt.xlabel ('alpha)
plt.ylabel ('$ || \mathbf {w} || ^ 2_2$')
plt.title ('Norma de los coeffs en función de la regularización')
plt.axis ('tight")
plt.show ()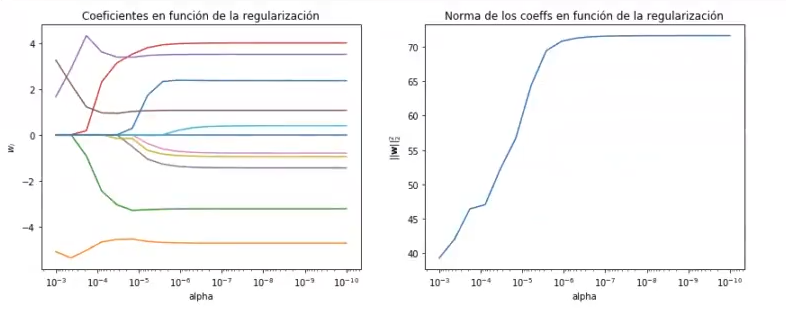

Si cambiamos el alphas = np.logspace (-10, -3, n_alphas) por alphas = np.logspace (-10, 3, n_alphas), para que la regularización suba hasta 10, 3, que es 1000, sí podemos observar cómo todos los coeficientes terminan con tendencia hacia 0:

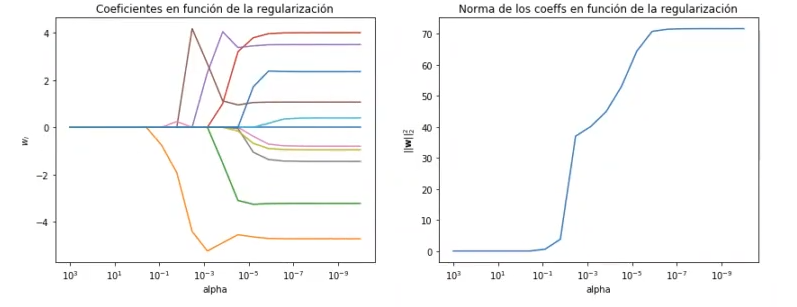
#Entrenar un modelo Lasso
from sklearn.model_selection import GridSearchCV

alpha_vector= np. logspace (-10, 1, 25)

alpha_vector = np. logspace (-15, 1, 25)
param_grid = {'alpha': alpha_vector}
grid = GridSearchCV (Lasso (), scoring = 'neg_mean_squared_error', param_grid = param_grid, cv = 5)
grid.fit(x_train, y_train)
print ("best mean cross-validation score: {:.3f}".format (grid.best_score_))
print ("best parameters: {}".format (grid.best_params_))

scores =1 np.array (grid.cv_results_ ['mean_test_score'])
plt.semilogx (alpha_vector, scores, ' -o ')
plt.xlabel ('alpha, fontsize = 16)
plt.ylabel ('5-Fold MSE')
plt.ylim ((0, 1))
plt.show ()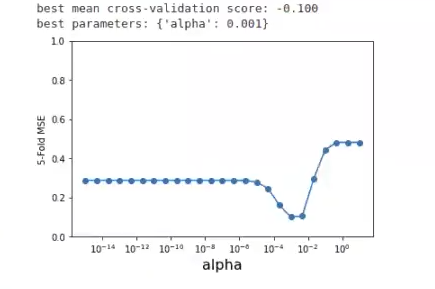

Vemos que el alfa más bajo es 0.01. Si ejecutamos el modelo con este valor de alfa, el resultado que obtendríamos sería:

#Entrenar un modelo Lasso
alpha_optimo = grid.best_params_['alpha']
lasso = lasso (alpha = alpha_optimo).fit (X_train, y_train)

#predicción
y_hat = lasso.predict (x_test)
W = lasso.coef
norm_w2= np.dot (w, w.T)

#error
error_test = np.mean (np.power (y - y_hat, 2))

plt.plot (x, g_x, 'r', label = '$y$')
plt.plot (x_, y_i, 'b.', label = '$y_i$")
plt.plot (x, y_hat, 'g', label = '$\hat {y} $')
plt.title ('Grado: %i, MSE:%.2f\nalpha: %g, $ l | w l |_2 ^ 2$.2g'% (degree.error_test, alpha_optimo, norm_v2))
plt.legend ()
plt.xlim (0, 2))
plt.ylim ((-2, 2))
plt.show ()

coef names = ['w' + str (i) + ' :  ' for i in range (1, degree + 1)]

for f, wi in zip (coef names, w):
print (f, wi)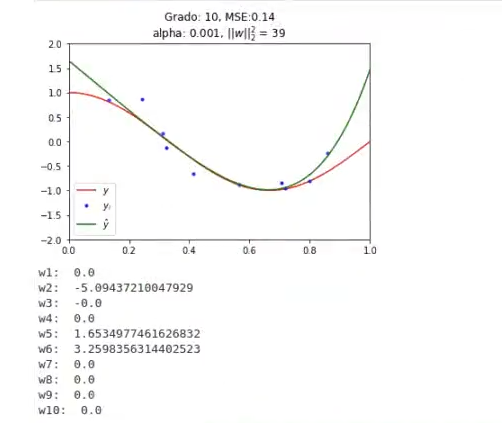

Como podemos observar, no es mucha la diferencia entre este modelo y el modelo sin regularizar.

¿Qué sigue?

Como hemos visto, entrenar un modelo Lasso es una tarea muy similar a entrenar un modelo Ridge. Si quieres seguir aprendiendo sobre estas temáticas, tenemos para ti una oportunidad única: el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación de alta intensidad en donde adquirirás todos los conocimientos necesarios para incursionar en el mercado laboral en pocos meses. ¡Anímate a transformar tu vida y solicita más información!