¿Sabes qué ocurre cuando hay errores que no siguen una distribución normal en estadística?
Es normal encontrarnos ecuaciones en donde el valor de Y va entre [-∞ , ∞], pero si tratamos de predecir un valor binario (si/no) o el número personas que circulan por una calle, por ejemplo, nos salimos de ese rango de distribución de Gauss.
Antes de ver los errores que no siguen una distribución normal en estadística
Estas desviaciones de la normalidad tienen una función de distribución de probabilidad distinta, que se sale un poco o mucho de las desviaciones típicas de la probabilidad normal.
Es en estos casos cuando utilizamos modelos lineales generalizados, es decir, un modelo normal. Utilizamos una función de enlace g(y) (link function) que transforma los resultados:
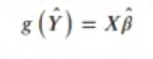
La función XB la transformamos en una función g (Y). Esto no retornará el resultado de la función normal, sino que va a dar un resultado transformado.
Su inversa sería g -1 ():
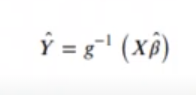
La g es lo que se conoce con el nombre de link function o función de enlace. En los errores que no siguen una distribución normal en estadística, esta función cumple la función de ajuste o conector entre los predictores en un modelo y el valor esperado de la variable dependiente de forma lineal.
La función de enlace conecta componentes y valores aleatorios con valores no aleatorios de un GLM.
Dependiendo de las distribuciones, vamos a tener que utilizar distintas funciones de enlace que arreglen los errores que no siguen una distribución normal en estadística.
Tipos de errores que no siguen una distribución normal en estadística
Distribución Bernoulli
La distribución de Bernoulli es una distribución de probabilidad discreta que puede tomar dos valores uno con probabilidad p y otro q = 1 –p. Se utiliza para describir sucesos que solo tienen dos posibles resultados como Si / No, 1 / 0 o Cara / Cruz.
Estimadores media (μ) y varianza (σ²):
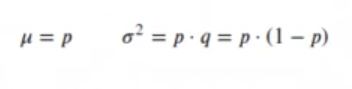
La función de densidad de probabilidad en los errores que no siguen una distribución normal en estadística se puede representar como:
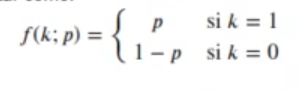
Donde k solo admite dos posibles valores k E {0, 1}.
Esta formula también se puede expresar como:
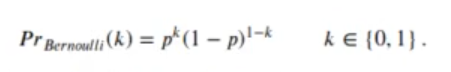
La distribución de Bernoulli es un caso especial de la distribución binomial con n = 1.
Distribución binomial
Si tenemos n sucesos independientes que siguen una distribución de Bernoulli, ¿cuál es la probabilidad de que k sucesos sean positivos?
Al tener k sucesos, donde k E (0, 1, 2…, n), la función será la de Bernoulli multiplicada por el coeficiente binomial que acabamos de ver:
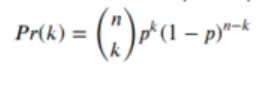
Función enlace – Logit
Tenemos que forzar a la regresión lineal al rango [0, 1]. Esto lo podemos conseguir con la función logística o sigmoide:
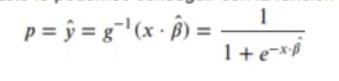
Su inversa en los errores que no siguen una distribución normal en estadística se conoce como la función logit:
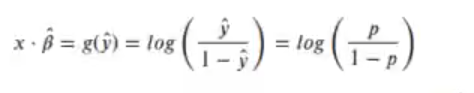
De donde sacamos que la solución de la regresión lineal era el logaritmo de la razón de monomios:
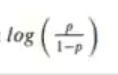
In [ ] : options (repr.plot.height = 4, repr.plot.width = 6)
y <- seq (-10, 16, length.out = 100)
xb <- 1 / (1 + exp (-y))
plot (y, xb, t = "l")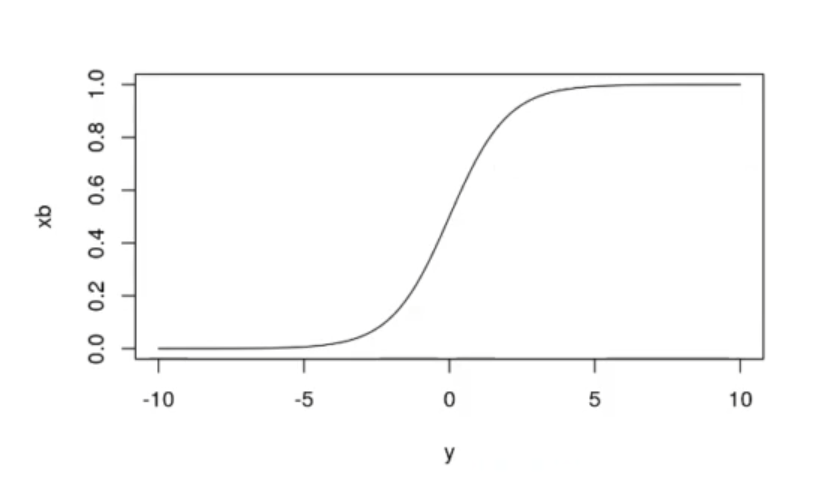
Cuando los valores de x . B son muy altos, nos va a dar una probabilidad cercana a 1; cuando son muy bajos, por el contrario, nos va a dar una probabilidad muy cercana a 0.
Interpretación de los coeficientes
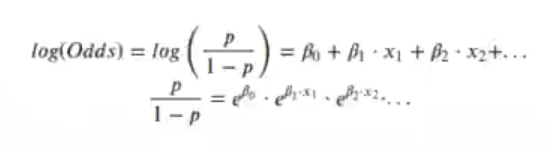
Expliquemos esta fórmula un poco:
Tenemos la regresión logística, que corresponde a β0 + β1 . x1 + β2 . x2 +…
El logaritmo (log (Odds)) de la regresión logística, de la razón de momios, es lo que nos da la regresión lineal.
Entonces, si lo deshacemos, lo que tenemos es que la probabilidad entre 1 – p es el exponente de los coeficientes. Las sumas pasan a multiplicaciones. Esto significa que si aumentamos β0, aumentamos también la razón de momios: eβ0. No estamos sumando, estamos multiplicando.
Lo mismo sucede si estamos aumentando el valor de β1; sabemos que por cada incremento de x1, la razón de momios se va a multiplicar por eβ1.
Así pues, solucionamos el problema de los errores que no siguen una distribución normal en estadística.
Ahora que entendemos qué podemos hacer cuando hay errores que no siguen una distribución normal en estadística y en Big Data, podemos dar el siguiente paso. Para ello, te invitamos a inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que en muy poco tiempo dominarás todos los conocimientos necesarios para incursionar en el mercado laboral con más oferta en la actualidad y, así, convertirte en un gran científico de datos. ¡No esperes para solicitar más información!











