Machine Learning Linear Regression es un modelo que aprende una relación en línea recta entre variables para predecir un valor numérico de forma simple e interpretable.
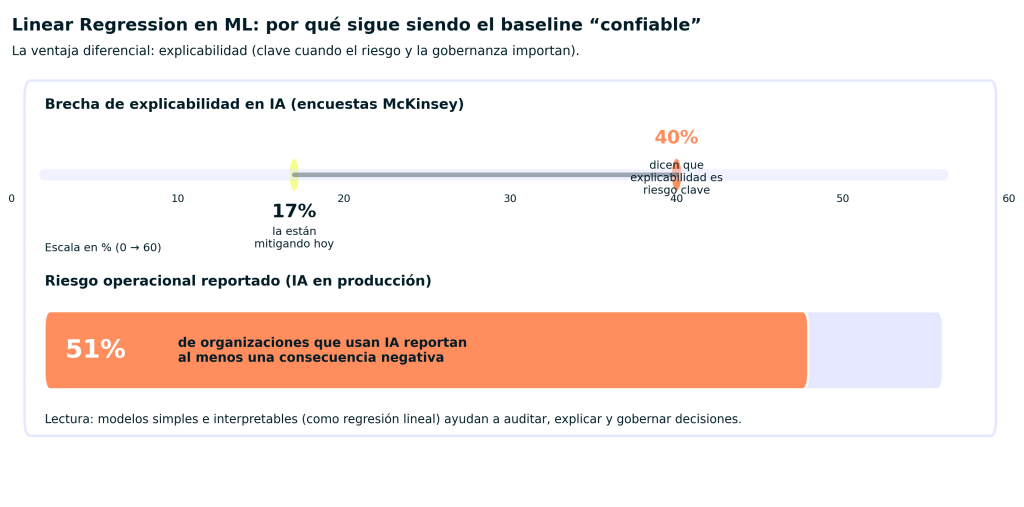
McKinsey reporta que 40% de organizaciones ve la explicabilidad como un riesgo clave al adoptar GenAI, pero solo 17% dice estar mitigándolo; además, 51% de organizaciones que usan IA reportó al menos una consecuencia negativa.
Cuando empecé a adentrarme en el mundo del machine learning, la regresión lineal fue mi primera parada. No sólo porque es uno de los algoritmos más sencillos, sino porque ofrece una base sólida para entender cómo funcionan muchos modelos predictivos. En este artículo quiero compartir contigo todo lo que necesitas saber sobre machine learning linear regression, desde los conceptos básicos hasta ejemplos prácticos y consejos para evitar errores comunes al aplicarla.
Qué Aprenderás Aquí
- Qué es exactamente la regresión lineal en machine learning y cómo funciona
- Por qué es un modelo fundamental para principiantes y profesionales
- Cómo implementarla paso a paso con ejemplos en Python usando Scikit-learn
- Métricas para evaluar tus modelos y evitar malentendidos
- Consideraciones prácticas y desafíos comunes a vigilar
- Recursos recomendados para profundizar tu aprendizaje
¿Qué es Machine Learning Linear Regression?
La regresión lineal es un método estadístico clásico que busca modelar la relación entre una variable dependiente y una o más variables independientes. En el contexto de machine learning, esta técnica se utiliza para la predicción, intentando encontrar la mejor línea (o hiperplano en múltiples dimensiones) que ajuste los datos de manera que pueda predecir valores futuros con precisión.
Matemáticamente, este modelo se representa así:
y = β₀ + β₁x₁ + β₂x₂ + … + βₙxₙ + ε
Donde:
- y es la variable objetivo, lo que queremos predecir.
- x₁, x₂, …, xₙ son las características o variables independientes.
- β₀ es el intercepto o término constante.
- β₁,…,βₙ representan los coeficientes que miden la influencia de cada variable.
- ε es el término de error, que significa la parte que no podemos explicar con el modelo.
Lo que el algoritmo hace es encontrar los valores de β que minimicen el error entre las predicciones y los datos reales — típicamente usando el método de mínimos cuadrados.
¿Por qué Elegir la Regresión Lineal en Machine Learning?
Desde mi experiencia, la regresión lineal es excelente para:
- Comprender relaciones básicas: Mejora significativamente el conocimiento de cómo variables se conectan.
- Modelos simples y efectivos: Con datos adecuados, ofrece resultados precisos sin complicaciones.
- Rapidez en entrenamiento y predicción: Ideal para datasets grandes o con recursos limitados.
- Interpretabilidad clara: Los coeficientes permiten analizar qué factores tienen mayor impacto.
- Base para técnicas avanzadas: Aprende regresión polinomial, regularización (como Ridge o Lasso) y otros modelos complejos desde aquí.
Esta combinación de simplicidad y utilidad práctica hace que sea mi técnica favorita para empezar proyectos de machine learning con datos tabulares.
Cómo Implementar Machine Learning Linear Regression con Scikit-learn

Permíteme mostrarte con un ejemplo real que usé recientemente para predecir precios de casas. Aquí tienes los pasos esenciales:
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# Simulamos datos (en la práctica usarías un dataset real)
X = np.array([[1500], [1600], [1700], [1800], [1900]]) # Superficie en pies cuadrados
y = np.array([300000, 320000, 340000, 360000, 380000]) # Precio en dólares
# Dividimos en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Creamos y entrenamos el modelo
model = LinearRegression()
model.fit(X_train, y_train)
# Realizamos predicciones
y_pred = model.predict(X_test)
# Evaluamos rendimiento
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f»Coeficiente: {model.coef_[0]:.2f}»)
print(f»Intercepto: {model.intercept_:.2f}»)
print(f»Error cuadrático medio (MSE): {mse:.2f}»)
print(f»Coeficiente de determinación (R²): {r2:.2f}»)
En menos de 15 líneas tenemos un modelo que puede predecir precios basándose en una sola característica. Imagínate usando múltiples variables, ¡las posibilidades se multiplican!
Métricas Clave para Evaluar Modelos de Regresión Lineal
En mi trabajo diario, siempre priorizo estas métricas:
- MSE mean squared error: Promedio de los errores al cuadrado, penaliza más los errores grandes.
- RMSE root mean squared error: Raíz cuadrada del MSE, más interpretable en unidades originales.
- R² coeficiente de determinación: Indica qué porcentaje de variabilidad de y es explicado por el modelo.
Llevar un buen seguimiento de estas nos asegura construir modelos robustos y evitar falsas ilusiones de precisión.
Desafíos y Recomendaciones Prácticas
Cada vez que aplico la regresión lineal, tengo en cuenta:
- Multicolinealidad: Variables independientes muy correlacionadas pueden confundir el modelo. Uso técnicas como análisis de correlación o eliminación de variables.
- Outliers: Datos atípicos afectan la línea de mejor ajuste. Realizo inspección gráfica y consideraciones para descartarlos o tratarlos.
- Validación cruzada: Para evitar un ajuste excesivo (overfitting), aplico validación cruzada y revisión de error en datos no vistos.
- Suposición de linealidad: Aseguro que los datos sean adecuadamente lineales o uso transformaciones para mejorar ajuste.
Con la experiencia, estos cuidados hacen la diferencia para que el modelo sea realmente útil.
Mi Experiencia Real: Un Caso de Uso
En un proyecto reciente con una startup dedicada al mercado inmobiliario, usamos regresión lineal para predecir precios de viviendas en función de características como tamaño, ubicación y número de habitaciones. Aunque el problema parecía simple, identificar variables redundantes y manejar outliers fue clave para aumentar el rendimiento del modelo en un 15% respecto a la versión inicial. Este aprendizaje me demostró que la teoría funciona, pero el toque humano y el análisis inteligente son imprescindibles para obtener resultados prácticos en machine learning
Conclusión: Empieza a dominar la regresión lineal hoy mismo
La machine learning linear regression no es solo un modelo sino una puerta de entrada fundamental al machine learning y la ciencia de datos. Su capacidad para explicar relaciones numéricas y realizar predicciones simples hace que sea una herramienta indispensable para desarrolladores y analistas.

Si quieres transformar tu carrera y aprender con proyectos reales, te recomiendo revisar el Bootcamp de Machine Learning de KeepCoding. Ahí no solo aprenderás regresión lineal, sino todo el ecosistema que necesitas para convertirte en un profesional destacado. Documentación oficial de Scikit-learn:
LinearRegression.











