Los métodos embebidos en machine learning o métodos embedded incorporan la selección de características como parte del proceso de entrenamiento, es decir, pueden utilizar algoritmos adecuados que permitan seleccionar características.

Los métodos embebidos en machine learning se pueden utilizar junto con técnicas hacia delante/atrás (métodos anidados) y suelen ser muy eficientes.

Algunos ejemplos de métodos embebidos en machine learning son:

Regularización Lasso.
Árboles de decisión/regresión.

¿Qué encontrarás en este post?

¿Qué podemos hacer con los métodos embebidos en machine learning?

Cada uno de los métodos de selección de características tiene sus distintas particularidades y estas van a depender mucho de las funciones que deseemos llevar a cabo. De modo que:

Técnicas de filtrado: filtrar (eliminar) las características poco relevantes en función de distintos criterios.
Técnicas wrapper: utilizar estrategias greedy para selección de características.
Técnicas embebbed: utilizar las particularidades de un algoritmo para seleccionar las características relevantes.

Ejercicio de aplicación

Vamos a hacer nuestro ejercicio con un dataset de House Sales disponible en Kaggle:

#Métodos embebidos en machine learning
#cargamos datos
house_data = pd.read_csv ("./data/kc_house_data.csv") #cargamos fichero

#Eliminamos las columnas id y date
house_data = house_data.drop (['id', 'date'], axis = 1)

#convertir las variables en pies al cuadrado en metros al cuadrado
feetFeatures = ['sqft_living' ,'sqft_lot', 'sqft_above', 'sqft_basement', 'sqft_living15', 'sqft_lot15']
house_data [feetFeatures] = house_data [feetFeatures].apply (lambda x: x * 0.3048 * 0.3048)

#renombramos
house_data.columns = ['price', 'bedrooms', 'bathrooms', 'sqm_living', 'sqm_lot', 'floors', 'waterfront', 'view', 'condition", 'grade', 'sqm_above', 'sqm_basement', 'yr built', 'yr_renovated', 'zip_code', 'lat', 'long', sqm_living15', 'sqm_lot15']

#añadimos las nuevas variables
house_data ['years'] = 2015 - house_data ['yr_built']
house_data ['bedrooms_squared'] = house data ['bedrooms'].apply (lambda x: x ** 2)
house_data ['bed_bath_rooms'] = house_data ['bedrooms'] * house_data ['bathrooms']
house datal ['log_sqm_living'] = house_data ['sqm_living'].apply (lambda x: np.log (x))
house_data ['lat_plus_long'] = house_data ['lat'] * house_data ['long']

house_data.head ()

#Métodos embebidos en machine learning
#convertimos el DataFrame al formato necesario para scikit-learn
data = house_data.values

y = data [ : , 0 : 1] #nos quedamos con la 1 columna, price
X = data [ : , 1 : ]  #nos quedamos con el resto

feature_names = house_data.columns [1 : ]

#Métodos embebidos en machine learning
from sklearn import preprocessing
from sklearn.model_selection import train_test_split

https://scikit-learn.org/stable/modules/generated/ sklearn.preprocessing.StandardScaler.html

#Dividimos los datos en entrenamiento y test (88 training, 20 test) Cuidado! En la vida real, el split se hace SIEMPRE ANTES del análisis exploraorio
X_train, X_test, y_train, y_test = train_test_split (x, y, test_size = .25, random_state = 2)

print (Datos entrenamiento: ' , X_train, shape)
print ('Datos test: ' , X_test.shape)

#Escalamos (con los datos de train)
scaler = preprocessing.StandardScaler().fit (X_train)
XtrainScaled = scaler, transform (X_train)
XtestScaled = scaler.transform (X_test)

En este caso, utilizamos la capacidad de Lasso para seleccionar variable.

#Métodos embebidos en machine learning
from sklearn.model selection import GridSearchCV
from sklearn.linear_model import Lasso

alpha_vector = np.logspace (-1, 10, 50)
param_grid = {'alpha': alpha_vector}
grid = GridSearchCV (Lasso (), scoring = 'neg_mean_squared_error', param_grid = param_grid, cv = 5)
grid.fit (XtrainScaled, y_train)
print ('best mean cross-validation score { : . 3f)'.format (grid.best_score_))
print ('best parameters: {}'.format (grid.best_params))

#-1 porque es negado
scores = -1 * np.array (grid.cv_results_['mean_test_score'])
plt.semilogx (alpha_vector, scores, '-o')
plt.xlabel ('alpha', fontsize = 16)
plt.ylabel ('5-Fold MSE')
plt.show ()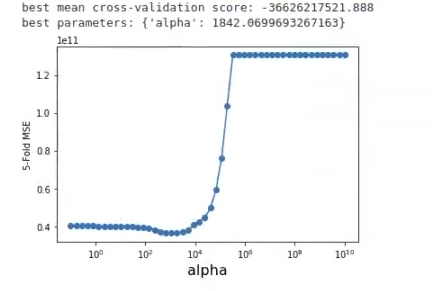

#Métodos embebidos en machine learning
from sklearn.metrics import mean_squared_error

alpha_optimo = grid.best_params_ ['alpha']
lasso = Lasso (alpha = alpha_optimo).fit (XtrainScaled, y_train)

ytrainLasso = lasso.predict (XtrainScaled)
ytestLasso = lasso.predict (XtestScaled)
mseTrainModelLasso = mean_squared_error (y_train, ytrainLasso)
mseTestModelLasso = mean_squared_error (y_test, ytestLasso)

print ('MSE Modelo Lasso (train): %0.3g' % mseTrainModelLasso)
print ('MSE Modelo Lasso (test): %0.3g'% mseTestModelLasso)

#print('RMSE Modele Lasso (train): se.3g np.sqrt(mseTrainMode(Lasso))
#print("RMSE Modelo Lasso (test) 80.3g & np. sqrt (ase TestModelLasso))

W = lasso.coef

for f, wi in zip (feature_names, w):
print (f, wi)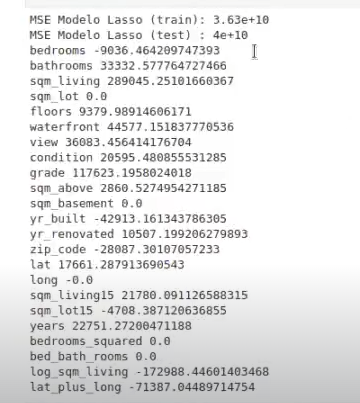

Como puede apreciarse, con este algoritmo hemos conseguido desactivar algunas variables (sqm_lot, sqm_basement, long, bedrooms_squared, bed_bath_rooms), lo que mejora la interpretabilidad del modelo a costa de aumentar ligeramente el error en test con respecto al método Ridge.

No obstante, siguen apareciendo algunas incoherencias con respecto al valor de los coeficientes, como, por ejemplo, el asociado a la variable bedrooms, que tiene valor negativo.

Si aumentamos el parámetro de regularización y observamos los resultados obtenidos, hemos aumentado el error, pero a cambio:

Tenemos un modelo más sencillo (menos variables al haber muchos coeficientes nulos) y, por tanto, menos susceptible a sufrir overfitting.
Mejoramos la interpretabilidad del modelo, las variables supervivientes (con coeficiente distintos de cero) parecen concordar con nuestra intuición sobre problema a resolver.

Una vez llegados a este punto, ¿qué podemos hacer? El error de entrenamiento/validación y test es similar, pero todavía es muy alto, así que:

Se podrían definir nuevas variables que nos ayuden a mejorar el error de predicción (MSE).
Jugar con el parámetro de regularización para mantener el compromiso entre sencillez/interpretabilidad del modelo y error de predicción (MSE).

Si quieres seguir aprendiendo sobre una de las disciplinas más interesantes y demandadas del mundo tech, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de 8 meses de duración en la que aprenderás toda la fundamentación teórica y práctica que te llevará a poder incursionar en el mercado laboral y cumplir tus sueños. ¡No esperes más, solicita información ahora!