Si estás trabajando con modelos de clasificación en machine learning, tarde o temprano te toparás con la curva ROC. Y cuando eso ocurra, necesitas entenderla bien. No solo porque aparece en casi todos los papers y dashboards de evaluación, sino porque es una de las herramientas más efectivas para medir el rendimiento de un modelo. En este artículo te explico de forma clara, con ejemplos y sin rodeos, qué es la curva ROC, cómo se interpreta, qué significa el AUC y cuándo usarla.

¿Qué encontrarás en este post?

¿Qué es la curva ROC?

La curva ROC (Receiver Operating Characteristic) es una representación gráfica que muestra el rendimiento de un modelo de clasificación binaria al variar su umbral de decisión.

Se creó originalmente para analizar señales en radares militares, pero hoy en día es fundamental en estadística y aprendizaje automático. En esencia, muestra la relación entre la Tasa de Verdaderos Positivos (TPR) y la Tasa de Falsos Positivos (FPR) en diferentes puntos de corte.

Eje X: Tasa de Falsos Positivos (FPR)
Eje Y: Tasa de Verdaderos Positivos (TPR)

Cada punto de la curva representa una combinación de TPR y FPR para un determinado umbral de clasificación.

¿Por qué es útil la curva ROC?

Porque permite visualizar qué tan bien distingue un modelo entre dos clases sin depender de un umbral fijo (como 0.5). Mientras que otras métricas como la precisión o la exactitud pueden ser engañosas en datasets desbalanceados, la curva ROC y su área bajo la curva (AUC) ofrecen una visión más completa del rendimiento del modelo.

¿Cómo se interpreta la curva ROC?

La clave está en la forma de la curva:

Una curva perfecta pasaría por el punto (0,1), lo que indica 0 falsos positivos y 100% de verdaderos positivos.
Una línea diagonal indica un modelo aleatorio (AUC = 0.5).
Cuanto más cercana esté la curva al punto superior izquierdo, mejor es el modelo.

¿Qué es el AUC (Area Under the Curve)?

Es un valor entre 0 y 1 que resume la curva ROC en un único número.

AUC = 1.0: modelo perfecto
AUC = 0.5: modelo aleatorio
AUC < 0.5: peor que el azar

Un AUC alto significa que el modelo tiene una gran capacidad para discriminar entre clases.

Ejemplo práctico de curva ROC en Python

Para entenderlo mejor, te dejo un ejemplo sencillo con scikit-learn:

pythonCopiarfrom sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt

# y_true: etiquetas reales, y_scores: probabilidades predichas
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
auc = roc_auc_score(y_true, y_scores)

plt.plot(fpr, tpr, label=f'AUC = {auc:.2f}')
plt.plot([0, 1], [0, 1], linestyle='--', color='gray')
plt.xlabel('Tasa de Falsos Positivos')
plt.ylabel('Tasa de Verdaderos Positivos')
plt.title('Curva ROC')
plt.legend()
plt.show()

Este fragmento genera la curva ROC y calcula el AUC automáticamente.

¿Cuándo usar la curva ROC?

Cuando tienes modelos de clasificación binaria.
Cuando el conjunto de datos está desbalanceado.
Cuando te interesa explorar distintos umbrales de decisión.

Sin embargo, si estás más enfocado en la clase positiva o si las clases están muy desbalanceadas, puedes considerar también la curva Precision-Recall, que en algunos casos puede ser más informativa.

Diferencia entre curva ROC y otras métricas

Métrica	¿Depende del umbral?	¿Sensibilidad al balance de clases?
Precisión	Sí	Alta
Recall (TPR)	Sí	Media
Accuracy	Sí	Alta
Curva ROC (AUC)	No	Baja

Por eso, la curva ROC es muy usada en investigaciones y producción, especialmente cuando se quiere evaluar un modelo sin fijar un punto de corte específico.

Ejercicio práctico: Curva ROC

Por último, para poner en práctica todo lo comentado anteriormente y, que de esta forma, interiorices todas las claves sobre la curva ROC a continuación, realizaremos un ejercicio práctico en el que aplicaremos la curva ROC a una matriz de confusión. Para ello, pintaremos la probabilidad de true positive y false positive.

In [46] : <- 4
radar_pred <- predict (model, radar.test)

df_preds <- data.frame (pred = radar_pred,
tipo_pred = factor (ifelse (radar_pred < umbral, 0, 1), labels = c ("ruido", "avión")),
tipo_real = radar.test$tipo)
df_preds <- df_preds [order (df_oreds$pred, decreasing = FALSE) , ]

M <- table (df_preds$tipo_real, df_preds$tipo_pred)
#table (real = radar.test$tipo, elegimos = y_est)

#Recall, Exhaustividad, Tasa Verdadero positivo
truePositive <- M [2, 2] / (M [2, 2] + M [2, 1])

#Tasa Falso positivo
falsePositive <- M [1, 2] / (M [1, 2] + M [1, 1])
paste ("tp:", truePositive, "fp:", falsePositive)
M

df_preds

‘tp: 0.363636363636364 fp: 0’

	pred	tipo_pred	tpo_real
	<dbl>	<fct>	<fct>
14	-12.998054	ruido	avión
49	-12.212471	ruido	avión
5	-10.568399	ruido	avión
52	-8.774266	ruido	avión
4	-5.860805	ruido	avión
42	1.181265	ruido	avión
30	1.605634	ruido	avión
10	1.763440	ruido	avión
22	2.499537	ruido	avión
7	2.604227	ruido	avión
27	3.117978	ruido	avión
28	3.730055	ruido	avión
24	3.975999	ruido	avión
51	3.984776	ruido	avión
25	4.711617	ruido	avión
60	6.052678	ruido	avión
35	7.213312	ruido	avión
31	9.375621	ruido	avión

In [47] : calctp_fp <- function (y_predict, y_real, th) {
y_est <- ifelse (y_predict < th, 0, 1)

M <- table (y_real, y_est)
#print (M)
if (ncol (M) == 2 & nrow (M) == 2) {
truePositive <- M [2, 2] / (M [2, 2] + M [2, 1])
falsePositive <- M [1, 2] / (M [1, 2] + M [1, 1]) 
c (tp = truePositive, fp = falsePositive)
} else {
c (tp = NA, fp = NA)
    }
}

In [48] : calctp_fp (df_preds$pred, df_preds$tipo_real, th = -1)

0.285714285714286

In [49] : dfROC <- data.frame (th =unique (df_preds$pred), tp = NA, fp= NA, model = "model1")

#for (th in seq (min (df_preds$pred), max (df_preds$pred), lenght.out = 10)) {
#calctp_fp (df_preds$pred, df_preds$tipo_real, th = th)
# }
for (i in 1 : nrow (dfROC)) {
v <- calctp_fp (df_preds$pred, df_preds$tipo_real, th = dfROC$th [i])
dfROC$tp [i] <- v ["tp"]
dfROC$tp [i] <- v ["fp"]
}
ggplot (data = dfROC, aes (x = fp, y = tp)) + geom_path ()

Warning message:

«Removed 1 row (s) containing missing values (geom_path).»

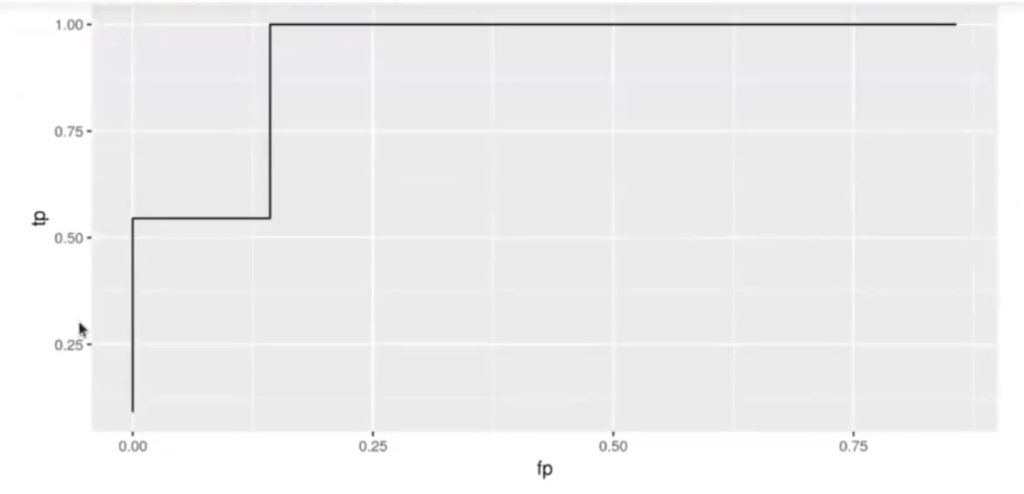
La curva ROC sale tan escalonada porque tenemos pocas muestras. Vamos a probar con un dataset más grande:

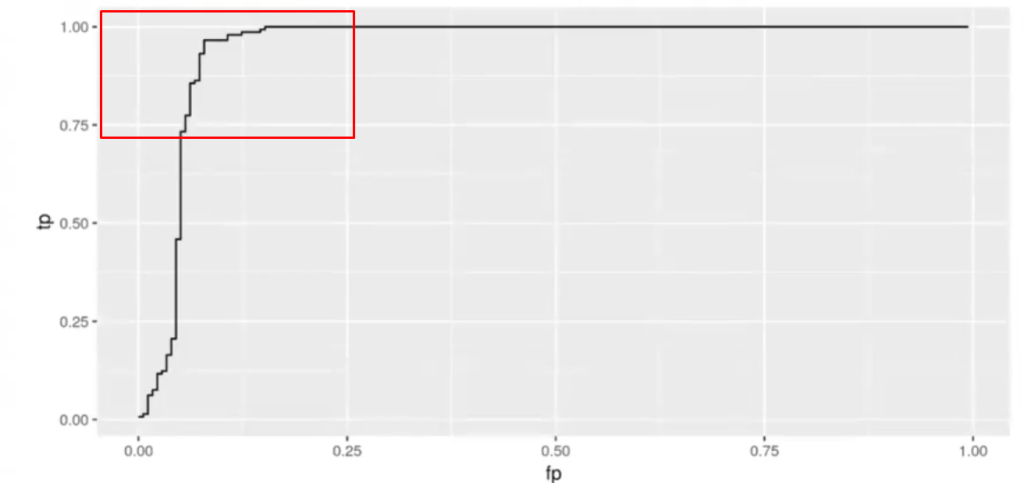
En función de qué clasificador quisiéramos con la curva ROC, nos interesaría más o menos estar por el área señalada en el recuadro rojo.

In [53] : library (ROCR)

#p <- predict (model_radar1, radar_big.test, type = "response")
p <- predict (mode_radar1, radar_big.test)

pr <- prediction (p, radar_big.tests$tipo, label.ordering = c ("ruido", "avion"))
prf <- performance (pr, measure = "tpr", x.measure = "fpr")
plot (prf, colorize = TRUE)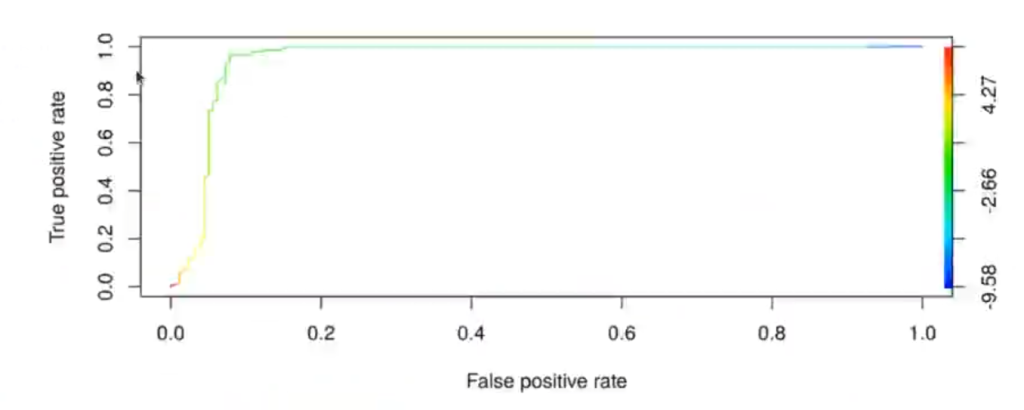

In [62] : pauc2 <- performance (pr2, measure = "auc", label.ordering = c ("ruido", "avión"))
[email protected] [[1]]

0.953170694166538

In (63): #library(pROC)
rocobjl <- PROC::roc(
radar_big.test$tipo,
predict (model_radar1, radar_big.test))

rocobj2 <- PROC::roc (
radar_big.test$tipo,
predict (model_radar2, radar_big.test),
levels = c ("ruido", "avion"), direction = "<")

#plot (rocobjl, print.auc = TRUE, col = "blue")
#plot(rocob)2, print.auc = TRUE, col = "green", print.auc.y = .4, add = TRUE)

pROC :: ggroc (list (model1 = rocobj1, model2 = rocob12), alpha = 0.5, size = 2) + xlab ("1 ~ FPR") + ylab ("TPR") + geom_abline (slope = 1, intercept = 1, alpha = 0.5)+
scale_colour_manual (values = c ("red", "#0000FF"), name = "Modelo", labels = c (paste0 ("Modelo1, AUC: " , PROC :: auc (rocobj1)),
paste0 ("Modelo2, AUC, PROC :: auc (rocobj2))))

Setting Levels: control = ruido, case = avion

Setting direction: controls < cases

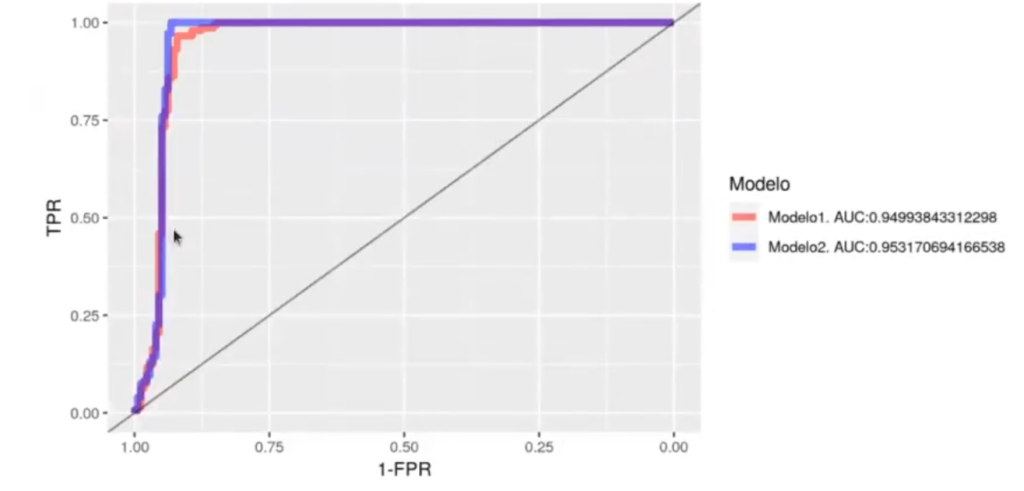
Conclusión sobre la curva ROC

Ya hemos visto qué es la curva ROC, cuál es su origen y cómo funciona, ¿ahora qué te parece si seguimos aprendiendo sobre estadística, Big Data y data mining? Para ello, desde Keepcoding te ofrecemos nuestro Bootcamp Machine Learning, con el cual en muy poco tiempo dominarás todos los conocimientos necesarios para convertirte en un gran científico de datos y acceder a las mejores ofertas laborales del mercado. ¡Anímate a impulsar tu carrera y solicita más información!