¿Sabes en qué consiste y cómo podemos calcular el rango de una matriz? En este artículo te haremos una pequeña introducción de este concepto.
Rango de una matriz
El rango de una matriz es la cantidad de información única que contiene nuestra matriz.
Veamos una pequeña ampliación de esta explicación, basada en un ejemplo.
Supongamos que tenemos la siguiente matriz:
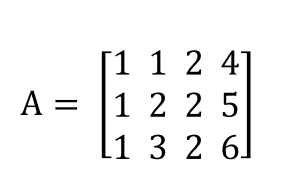
¿Cuál crees que es el rango de una matriz como esta?
Hay que tener en cuenta un factor: la primera columna es linealmente dependiente de la segunda. Es decir, si multiplicamos 2 por la primera columna, nos va a dar como resultado los valores de la tercera columna.
Entonces, podríamos pensar en suprimir la primera columna, pero si nos fijamos detenidamente, la suma de las tres primeras nos da la última.
Ejercicio sobre el rango de una matriz
Imagina que has estado de viaje y que no has tenido cobertura. Llegas de nuevo a casa y has quedado con tus amigos, pero a distintas horas, porque ninguno de ellos coincide en una hora en común.
Entonces:
- El amigo 1 te pregunta por tus vacaciones y te cuenta varias cosas:
- Que se ha muerto su perro.
- Que ha encontrado un nuevo trabajo.
El amigo 1 se ha ido y llega el amigo 2.
- El amigo 2 te cuenta que:
- Se ha comprado una casa.
- También que al amigo 1 se le ha muerto el perro.
El amigo 2 se va y llega el amigo 3 a otra hora distinta.
- El amigo 3 te pregunta si sabes que:
- El amigo 2 se ha comprado una casa.
- Se muda a Alemania.
Entonces, aquí hay información que ya está repetida, como la compra de la casa y la muerte del perro, información compartida por diversos amigos.
En este caso hipotético, en donde tenemos 6 campos en la matriz, la cantidad de información única que hay, es decir, el rango, no es 6, porque hay información que ya han dicho otros personajes, sino 4.
La información repetida sería:
- Que el perro del amigo 1 se ha muerto.
- Que el amigo 2 se ha comprado una casa.
Esto, matemáticamente, viene expresado por la dependencia lineal. Es decir, las matrices que tenemos son:
- Linealmente dependientes: información que ya tendríamos en la matriz.
- Linealmente independientes: información que no tenemos.
¿Quieres seguir aprendiendo?
Ahora que sabes cómo funciona el rango de una matriz puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector. Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!











