La regresión lineal en estadística Big Data es uno de los tantos modelos de cálculo con los que podrás contar para guiar tu estudio estadístico, por lo que su importancia radica en que te ayudará a orientar la forma en la que se estudian ciertas variables presentadas en los macrodatos procesados.
En efecto, este tipo de sistemas cumplen el propósito de facilitar los procesos y asegurar resultados más precisos, gracias a los que se destaca el valor de la información. Por este motivo, en este post, te explicamos qué es y cómo funciona la regresión lineal en estadística Big Data.
Regresión lineal en estadística Big Data
La regresión lineal en estadística Big Data es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente Y, la variable independiente X y un término aleatorio ε.
Por otra parte, este modelo puede expresarse con la siguiente fórmula:
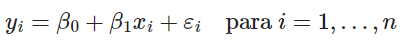
Por ejemplo
Con el fin de comprender cómo se utiliza la regresión lineal en estadística Big Data, a continuación, te ejemplificamos el desarrollo de su inscripción por medio del lenguaje de programación R:
options(repr.plot.height=5,repr.plot.width=8 , repr.plot.res = 400) n<-100 x<-rnorm(n,sd=1) y<- 1+20*x+rnorm(n,mean=1,sd=10) plot(x,y) abline(c(1,20),col="blue") grid()
Ahora, debido a las variables que utiliza, la forma de graficar sus resultados se da a través de un gráfico de dispersión, como el siguiente:
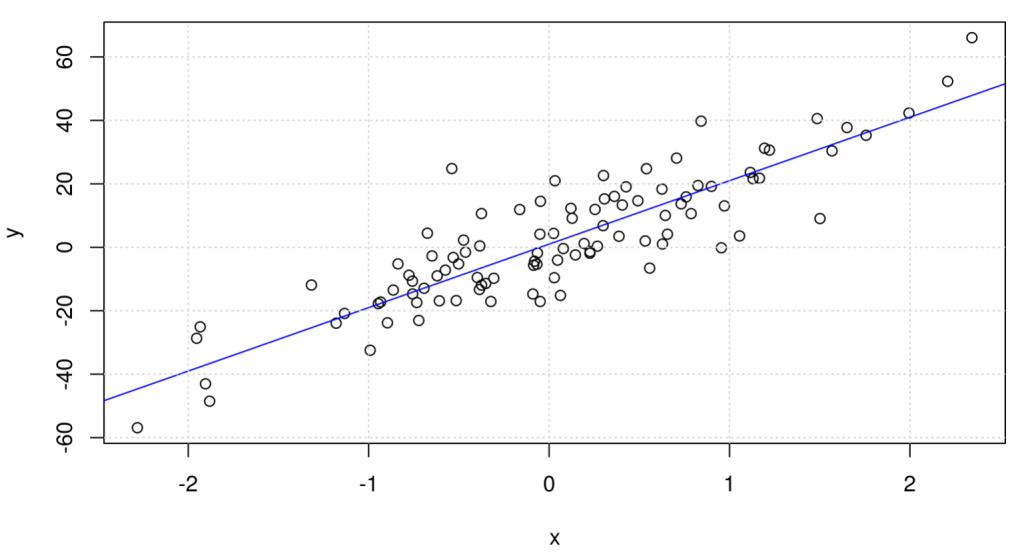
Esto significa que se puede expandir de la siguiente manera:
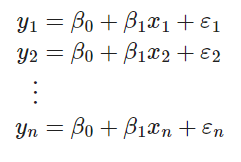
Donde:
- (Y sub i): i-esimo valor de la variable dependiente.
- (X sub i): i-esimo valor de la variable independiente.
- (ε sub 1): error, valor aleatorio.
- (β sub 0), (β sub 1): parámetros a determinar que dado un conjunto de X produce los mejores Y sub 1:
- (β sub 0): puede llamarse sesgo, bias, intercept o término constante. Indica el corte en el eje Y.
- (β sub 1): puede llamarse pendiente o slope. Indica cuánto aumenta Y por cada incremento de X.
Esto podrás escribirlo en forma de matriz: [ \begin{bmatrix} y_1 \ y_2 \ \vdots \ y_n.
\end{bmatrix}
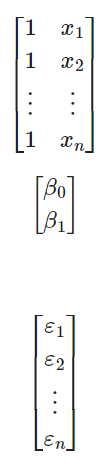
\] Lo que se puede simplificar como:
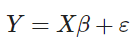
Donde:
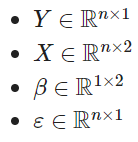
Por último, te compartimos otro ejemplo de la regresión lineal en estadística Big Data utilizando esta matriz:
n<-10
beta<-matrix(c(5,2),nrow = 2)
X<-matrix(c(rep(1,n),1:n),ncol = 2, byrow = F)
print("El valor de la matriz X es:")
X
print("El valor de la Beta es:")
beta
[1] “El valor de la matriz X es:”
A matrix: 10 × 2 of type dbl
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
[1] “El valor de la Beta es:”
A matrix: 2 × 1 of type dbl
5
2
print("El valor de la matriz X·Beta es:")
X %*% beta
[1] “El valor de la matriz X·Beta es:”
A matrix: 10 × 1 of type dbl
7
9
11
13
15
17
19
21
23
25
print("El valor final de la matriz Y es:")
e<-rnorm(n)
Y<-X %*% beta +e
Y
[1] "El valor final de la matriz Y es:"
A matrix: 10 × 1 of type dbl
| 8.289871 |
| 6.698527 |
| 10.712035 |
| 12.153768 |
| 13.162676 |
| 17.714525 |
| 18.830177 |
| 21.195451 |
| 24.414823 |
| 23.900571 |
plot(X[,2],Y,ylim = c(0,30)) abline(beta,col="blue") grid()
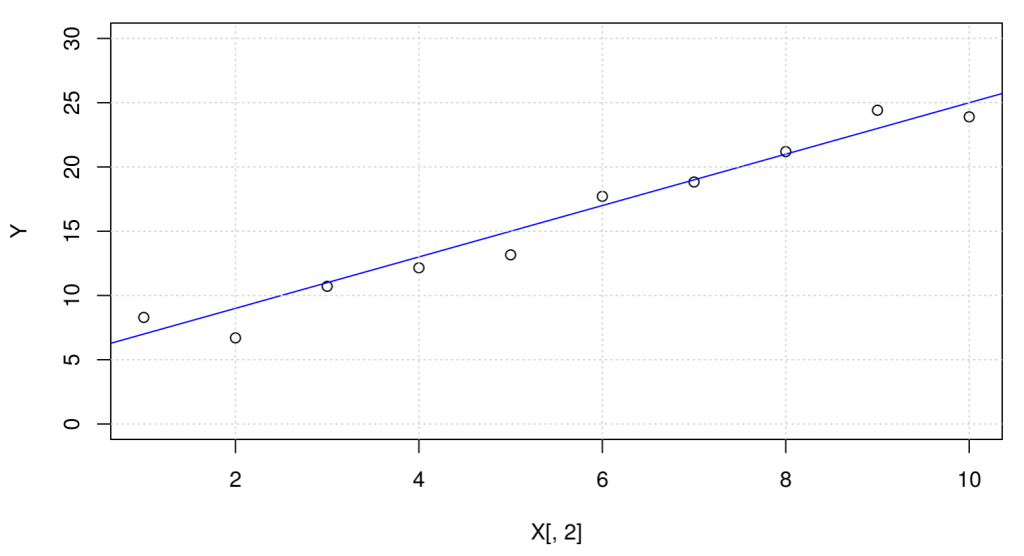
Por medio de este post, te hemos expuesto qué es y cómo funciona la regresión lineal en estadística Big Data; sin embargo, debes tener en cuenta que para llevar a cabo un análisis estadístico resulta necesario comprender muchos más factores y herramientas para que los resultados arrojados sean más asertivos.
Para aprender más sobre cada uno de estos, desde KeepCoding te ofrecemos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. En el transcurso de sus 11 módulos, aprenderás sobre fuentes de datos múltiples, visualización de relaciones entre valores numéricos (diagramas de dispersión, regresión y clustering), sobre tipos de datos específicos, como geográficos o mapas de calor… ¡Apúntate ahora!









