Representar el MSE para distintos niveles de complejidad

En este artículo vamos a representar el MSE para distintos niveles de complejidad de un algoritmo de regresión lineal (distintos grados del polinomio). Lo haremos tanto para train como para test.

Recordemos que el MSE hace referencia al mean squared error o error cuadrático medio, que nos dice lo cerca que está una línea de regresión de un conjunto de puntos.

Representar el MSE

Veamos, pues, cómo representar el MSE:

#Representar el MSE
N = 50
grado_polinomio = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
Nrepeticiones = 100
#Inicializamos
mse_test = np.zeros ((len (grado_polinomio), Nrepeticiones))
mse_train = np.zeros ((len (grado_polinomio), Nrepeticiones))
np.randon.seed (0)
for k in range (Nrepeticiones):
y = g_x + np.random.randn (N_test) * 1
idx = np.random.randint (0m N_test, N)
x_i = x [idx]
y_i = y [idx]
for j, d in enumerate (grado_polinomio):
_, mse_test [j, k], mse_train [j, k] = miRegresionLineal (x_i, y_i, x, y, d)
plt.plot (grado_polinomio, np.mean (mse_train, axis = 1), 'b', label = 'train')
plt.plot (grado_polinomio, np.mean (mse_test, axis = 1), 'r', label = 'test')
plt.legend ()
#plt.ylim ((0, 5))
plt.show ()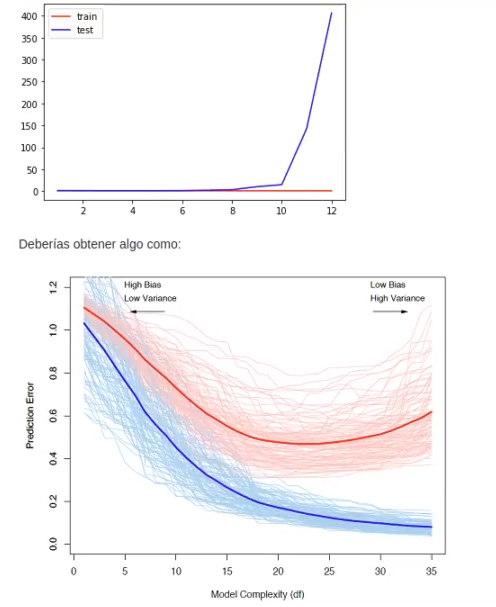

Estos serían los resultados si dejamos con comentario la penúltima línea que dice: #plt.ylim ((0, 5)). Aquí ambas gráficas han quedado similares, pero no se alcanza a ver muy bien, porque al representar el MSE de test, este es demasiado grande y el ejercicio se vuelve muy complejo. De modo que, si le quitamos el comentario a esa línea, nos mostraría resultados como estos:

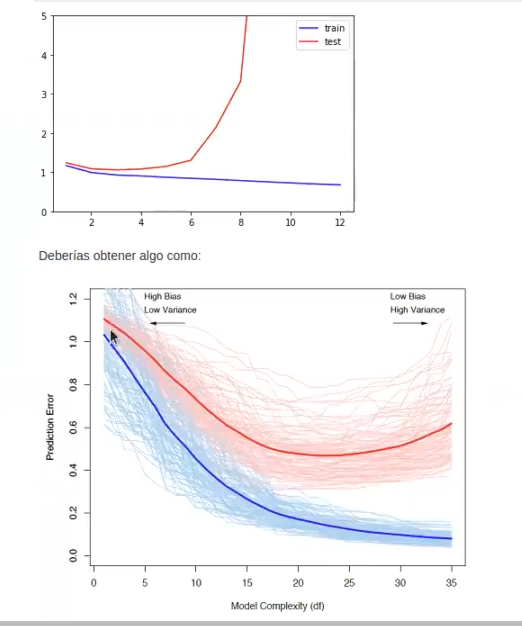
Al representar el MSE de test tenemos, por tanto, que a medida que aumenta, aumentamos también la complejidad del modelo. Este fenómeno se puede evidenciar en ambas gráficas, pero en la primera se ve más pronunciada la curva porque el error de test aumenta más rápido.

Al representar el MSE de train, por el contrario, va disminuyendo en ambas gráficas.

Teniendo en cuenta el lado derecho de la última gráfica y sabiendo que tenemos poco sesgo y mucha varianza, ¿podríamos decir que aquí hay overfitting o underfitting? La respuesta es overfitting.

Por tanto, examinando la diferencia en las prestaciones entre el conjunto de entrenamiento/validación y test, puedes saber si estás en alguna de las siguientes situaciones:

• Alto sesgo: error de entrenamiento/validación y error en test similar, pero muy alto. Cuando esto sucede podemos:
  • Aumentar el número de variables/características.
  • Aumentar el grado del polinomio (mayor complejidad).
• Alta varianza: gran diferencia entre error e entrenamiento/validación y test con un error de entrenamiento pequeño.
  • Aumentar el número de muestras de entrenamiento.
  • Reducir el número de variables/características.

Número de ejemplos disponibles

A raíz de la discusión anterior podemos pensar que, cuando tratamos con un problema muy complejo, utilizar más muestras de entrenamiento siempre nos va a ayudar, así que deberíamos dedicar muchos esfuerzos en conseguir muchos ejemplos. Pues bien, esto no es del todo cierto y, para demostrarlo, podemos representar las curvas de aprendizaje o learning curves. Estas representan la evolución de las prestaciones de un algoritmo supervisado (entrenamiento/validación y test) frente al número de muestras utilizadas.

Estas curvas tienen un aspecto como el siguiente:

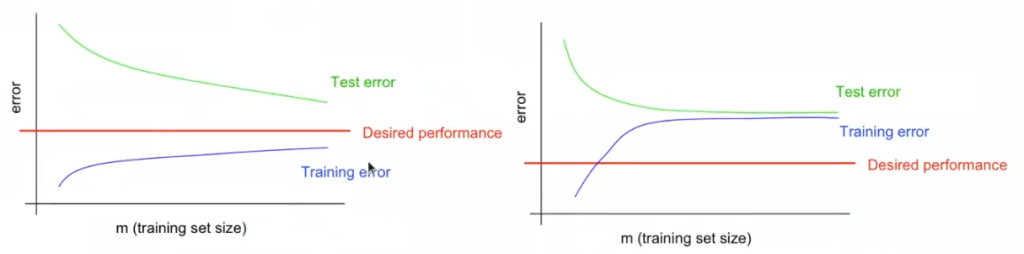
Si miramos la primera gráfica, parece que, a medida que aumentamos el train y el test, ambas curvas van acercándose al rendimiento deseado. Pero si miramos la segunda gráfica, vemos que no es así.

¿Podríamos decir cuál de las curvas anteriores se corresponde con un problema de alto sesgo/varianza? La segunda curva es la que tiene un error de sesgo/varianza muy alto, tanto en test como en training, por tanto esto es underfitting. La primera curva, en cambio, se va acercando a lo que se conoce como sweet spot.

Dimensionalidad

Hace referencia al número de características que podemos utilizar en un problema de aprendizaje automático.

Hay que tener en cuenta el principio de la maldición de la dimensionalidad. Este principio indica que, a medida que el número de variables o características aumenta, el número de muestras de entrenamiento que necesitamos para generalizar correctamente aumenta exponencialmente.

Así, también se puede controlar la complejidad (varianza), modificando el número de características. Técnicas como selección de características, resultan, por tanto, de utilidad.

Ahora que sabes cómo representar el MSE en distintos niveles de complejidad de los algoritmos de regresión lineal, ¡puedes seguir aprendiendo! Si te interesa el mundo del Big Data, tenemos para ti el Bootcamp Data Science, una formación intensiva en la que podrás adquirir todas las herramientas y conocimientos, tanto a nivel teórico como práctico, para seguir forjando tu futuro. ¡Atrévete a dar el paso que cambiará tu vida y solicita más información ahora!