Los análisis estadísticos te facilitan la comprensión de los datos, puesto que responden a las distintas preguntas que le realices al procesamiento del Big Data. En este post, te explicamos cómo funciona la fiabilidad de los coeficientes en estadística.
Fiabilidad de los coeficientes en estadística
Para exponer la fiabilidad de los coeficientes en estadística Big Data, vamos a partir de un ejemplo. Supón que los residuos siguen una distribución gaussiana, entonces se puede calcular la varianza de cada uno de los coeficientes como:
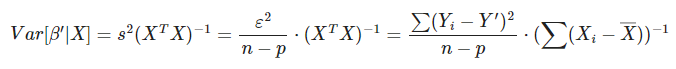
Donde:
- p es el número de grados de libertad, de coeficientes. En este caso son dos: intersección y pendiente.
- n es el número de muestras.
La media de los coeficientes viene dada por el vector β’. Con la media y la varianza podrás calcular la probabilidad de que el valor de la media estimado esté muy desviado de 0 por puro azar.
Eso aparece con el valor Pr(>|t|) en el summary del modelo: cuanto menor sea este valor, más fiable será.
vcov_matrix<-as.numeric(t(model$residuals)%*%model$residuals/(length(model$residuals)-2))*solve(t(X)%*%X)
# vcov_matrix <- vcov(model)
# 1/sum((X[,2]-colMeans(X)[2])^2) == solve(t(X)%*%X)[2,2]
paste("p-valor para intersección:",(1-pt(model$coefficients[1]/sqrt(diag(vcov_matrix))[1],8))*2)
paste("p-valor para pendiente:",(1-pt(model$coefficients[2]/sqrt(diag(vcov_matrix))[2],8))*2)
‘p-valor para intersección: 2.29549455081912e-05′
‘p-valor para pendiente: 1.32402191432845e-08′
vcov_matrix
Para averiguar la fiabilidad de los coeficientes en estadística, podrás calcular el margen de error para la intersección conociendo su desviación típica y que sigue una distribución t-student.
Para un intervalo de confianza del 95%, la fórmula de los márgenes superior e inferior es:
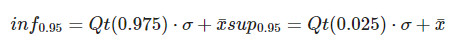
library(ggplot2)
options(repr.plot.height=2,repr.plot.width=6)
mydt<-function(x,df,mn,sd){
dt((x-mn)/sd,df)
}
df<-n-2
ggplot(data=datos, aes(x=X)) +
stat_function(fun=mydt,args = list(df = df,mn=model$coefficients[1],sd=sqrt(diag(vcov_matrix))[1]),color="#2222BB")+
geom_vline(xintercept=qt(0.975,df,lower.tail = F)*sqrt(diag(vcov_matrix))[1]+model$coefficients[1])+
geom_vline(xintercept=qt(0.025,df,lower.tail = F)*sqrt(diag(vcov_matrix))[1]+model$coefficients[1])+
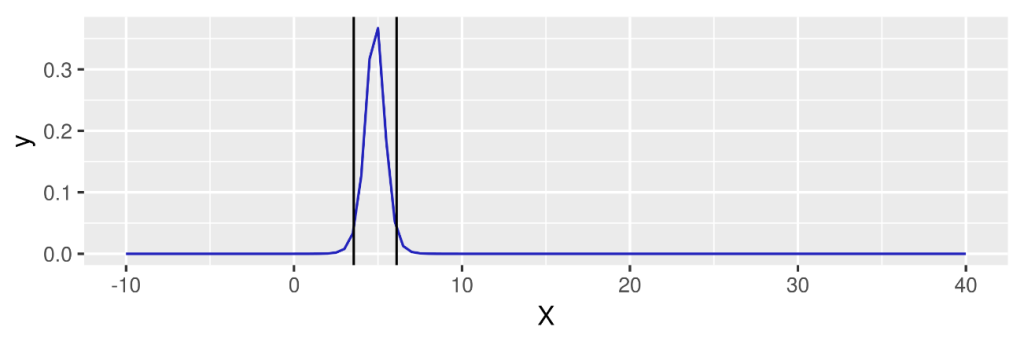
Con R podrás calcular esto automáticamente mediante el comando confint:
cnf_int<-confint(model) cnf_int
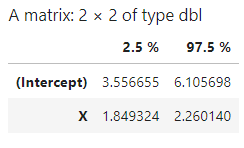
Por otra parte, para la fiabilidad de los coeficientes en estadística, tendrás que tener en cuenta los siguientes dos factores:
Opción interval = ‘confidence’
Un intervalo de confianza de la predicción es un rango que probablemente contiene el valor medio de la variable dependiente dados los valores específicos de las variables independientes. Estos intervalos proporcionan un rango para el promedio de la población. Estos rangos no dicen nada sobre la distribución de los puntos de datos individuales alrededor de la media de la población.
Opción interval = ‘prediction’
Un intervalo de predicción es un rango que probablemente contiene el valor de la variable dependiente para una sola observación nueva, dados los valores específicos de las variables independientes. Con este tipo de intervalo, estarás prediciendo rangos para observaciones individuales en lugar del valor medio.
pred_conf<-predict(model,datos,interval = 'confidence') head(pred_conf) pred<-predict(model,datos,interval = 'prediction') head(pred)
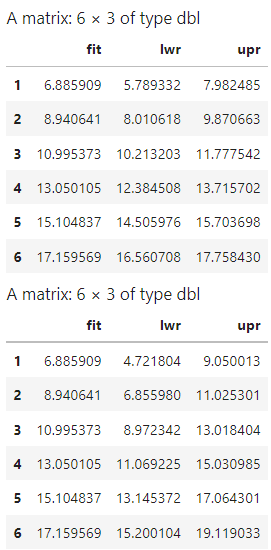
options(repr.plot.height=4,repr.plot.width=6) est_Y <- X %*% model$coefficients plot(X[,2],Y,col="blue") points(X[,2],est_Y,col="red") lines(X[,2],pred[,"fit"],col="red") lines(X[,2],pred_conf[,"lwr"],col="black") lines(X[,2],pred_conf[,"upr"],col="black") lines(X[,2],pred[,"lwr"],col="gray") lines(X[,2],pred[,"upr"],col="gray") #abline(c(5,2),col="green")
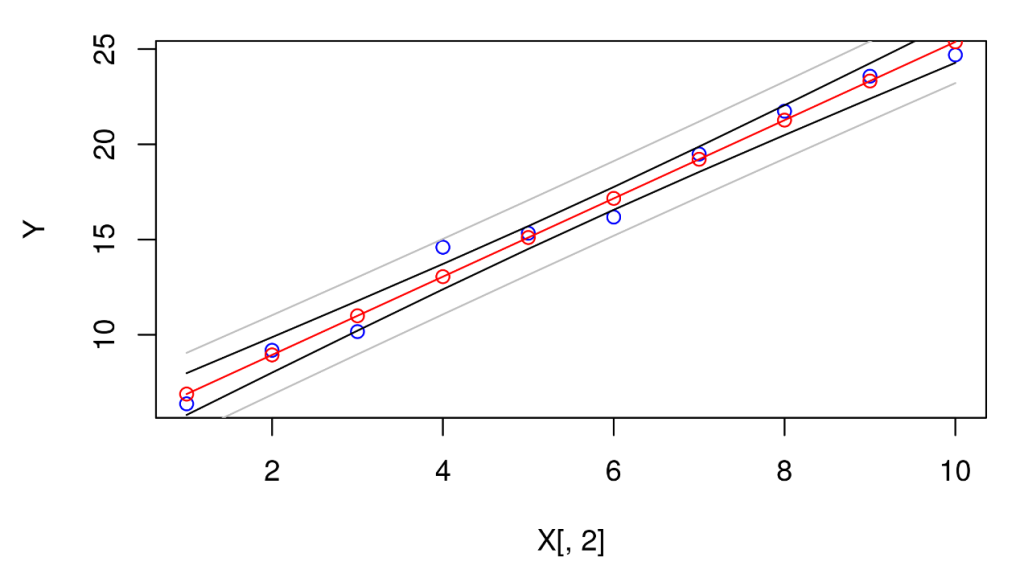
Ahora que sabes cómo funciona la fiabilidad de los coeficientes en estadística, te recodamos que existen muchos más estadísticos por aprender, por ello, ¡te animamos a seguir aprendiendo sobre el Big Data!
Como propuesta, te presentamos el Bootcamp Data Science. Durante el desarrollo del mismo, podrás instruirte en uno de los grandes retos para los data scientists, que ha sido el de ser capaces de elegir las características y herramientas adecuadas para solucionar cada problema en la gestión de los macrodatos. En menos de nueve meses, podrás convertirte en un experto en el manejo del Big Data. ¡Inscríbete ahora!











