En este artículo aplicaremos árboles de regresión a un ejemplo de regresión sintética.
Si has hecho machine learning seguro has escuchado mentar o, incluso te, te habrá tocado trabajar con árboles de decisión. ¿Por qué hacemos mención a estos tipos de árboles, si el tema de este post son los árboles de regresión? Pues bien, porque los árboles de regresión son, básicamente, árboles de decisión que se usan para regresión y pueden predecir salidas de valor continuo en lugar de salidas discretas.
Error cuadrático medio
En los árboles de clasificación veíamos cómo el árbol hacía preguntas correctas en el nodo correcto para brindar clasificaciones precisas y eficientes. Esto se logra gracias a la entropía y la ganancia de información. Debido a que en los árboles de regresión estamos prediciendo variables continuas, no es posible calcular la entropía y, por tanto, no se puede ganar información.
Lo que debemos buscar, pues, es una nueva medida que nos sirva para avisar cuánto se desvían nuestras predicciones de la variable objetivo u objetivo final. Esta es precisamente la finalidad del MSE (Mean Squared Error) o error cuadrático medio. Por tanto, en los árboles de regresión lo que buscamos es reducir el error cuadrático medio en vez de usar entropía, como en los algoritmos de clasificación.
Ejemplo de árboles de regresión
Veamos un ejemplo de árboles de regresión, para que lo entiendas mejor.
N_train = 10
N_test =100
#función verdadera g (x)
x = np.linspace (0, 1, N_test)
gx= np.cos (1.5 * np.pi * x)
# proceso y
np.random.seed (0) # para asegurar reproducibilidad
epsilon = np.random.randn (N_test) * 0.2
y = g_x + epsilon
#Datos: D = (x1, y1), obtenemos una muestra
idx = np.random.randint (0, N_test, N__train)
x_i = x [idx]
y_i = y [idx]
plt.plot (x, g_x, 'r', label = 'g (x)')
plt.plot (x1, y_i, 'b.', label = 'y')
plt.legend ()
plt.show ()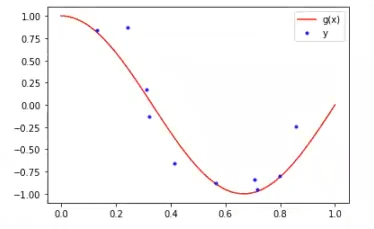
Este anterior es el ejemplo sintético.
Ahora el siguiente paso es importar el regresor (import DecisionTreeRegressor).
from sklearn.tree import DecisionTreeRegressor
X_train = x_1.reshape (-1, 1)
y_train = y_i
X_test = x.reshape (-1, 1)
regTree = DecisionTreeRegressor (max_depth = 2)
regTree.fit (x_train, y_train)
y_hat regTree.predict (x_test)
#error
error_test = np.mean (np.power (y - y_hat, 2))
plt.plot (x, g_x, 'r', label = '$y$')
plt.plot (x_i, y_i, 'b.', label ='$y_i$')
plt.plot(x,y_hat, 'g', label ='$\hat {y} $')
plt.title ('MSE: .2f' % error_test)
plt.legend ()
plt.xlim ((0, 1))
plt.ylim ((-2, 2))
plt.show ()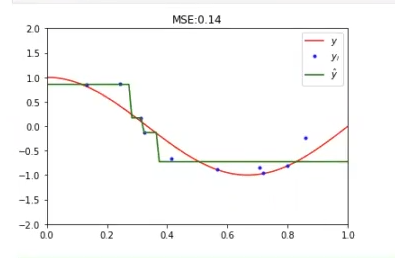
Esto es lo que nos queda. Si nos fijamos, este ejercicio de árboles de regresión tiene un max depth de 2. Observemos cómo queda con el max depth de 12:
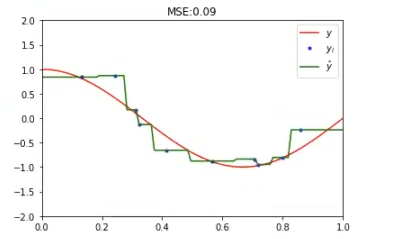
Lo que pasa es que esto se sobreajusta, es decir, está en overfitting.
Si en este momento cambiamos el DecisionTreeRegressor por un DecisionTreeClassifier, pueden suceder varias cosas. En nuestro caso nos ha salido error, porque es continuo. Estos son determinados casos no muy recurrentes, pero puede pasar.
Puede haber algunos casos en los que el clasificador acepte la variable porque no es totalmente continua, pero este no es nuestro caso, aquí ha sucedido todo lo contrario. En el caso de que sí pase, el algoritmo la toma como una clasificación multiclase, pero, por supuesto, el resultado de esa clasificación multiclase va a ser pésimo.
Al ser continua la variable, el clasificador no puede identificar un rango de números, ya que las variables continuas son aquellas que pueden tomar cualquier valor real dentro de un intervalo o rango.
Ahora miremos cómo podemos representar el árbol entrenado:
dot_data = tree.export graphviz (regTree, out file = None, feature_names = ['x'], filled = True, rounded = True, special_characters = True)
graph = graphviz.Source (dot_data)
graph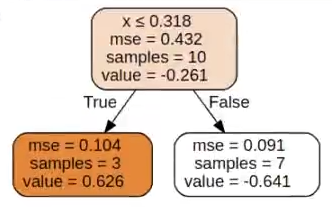
Esto es lo que tenemos. Si observamos y hacemos la comparación entre árboles de decisión normales y estos árboles de regresión, aquí ya no nos está dando el Gini, sino el mse y lo que tenemos aquí es el error cuadrático medio.
Si aumentamos el max_depth a 4, el resultado será algo como esto:
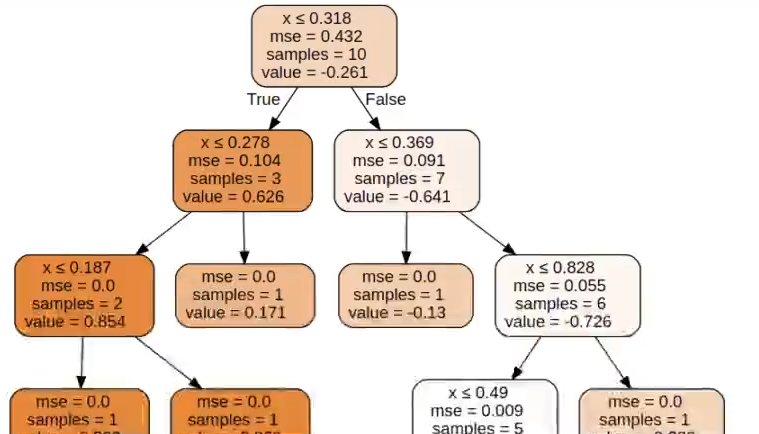
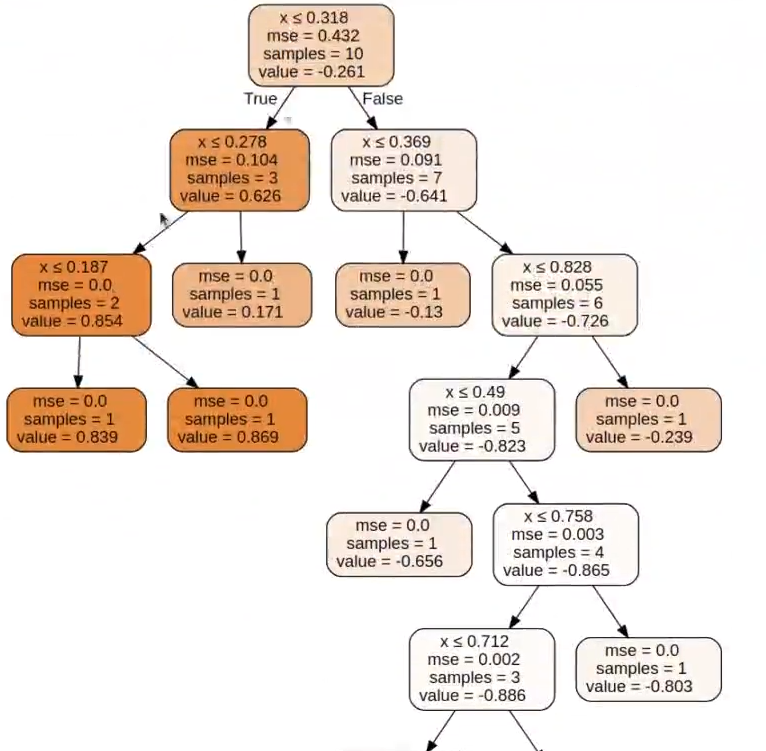
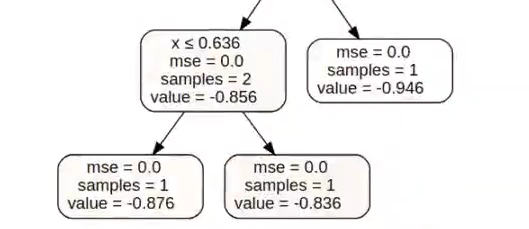
Si eliminamos por completo el max depth, lo que hace el algoritmo es llevar los árboles de regresión al tope y lo que tenemos es un árbol muy profundo, donde hay una clasificación perfecta como consecuencia de tener hojas con una única muestra.
El Big Data es, según portales como Glassdoor, una de las disciplinas mejor pagadas en la actualidad. Si te interesa profesionalizarte en ella, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de 8 meses de duración en la que podrás adquirir todos los conocimientos y herramientas necesarias para triunfar en el mercado laboral más prolífico de la actualidad. ¡Anímate a seguir tu camino hacia el éxito y solicita más información ahora!







